Potęgowanie

Potęgowanie – typ funkcji dwóch zmiennych, różnie definiowanych w różnych kontekstach; w najprostszych przypadkach – kiedy drugim argumentem tej funkcji jest liczba naturalna – potęgowanie to wielokrotne mnożenie elementu przez siebie^[1]. Podstawowe pojęcia związane z tą operacją to:

• podstawa potęgi – potęgowany element;
• wykładnik – drugi argument, w najprostszym przypadku równy liczbie czynników w mnożeniu;
• potęga elementu – wynik potęgowania;
• kwadrat – druga potęga;
• sześcian – trzecia potęga.

Potęgę zwykle zapisuje się, pisząc wykładnik po prawej stronie podstawy w indeksie górnym^[a]; przykładowo jeśli podstawą jest liczba 3, a wykładnikiem – liczba 4, to pisze się:

${\displaystyle 3^{4}:=3\cdot 3\cdot 3\cdot 3=81.}$

Nazwy drugiej i trzeciej potęgi nawiązują do geometrii, gdyż pole powierzchni kwadratu o boku długości ${\displaystyle a}$ wynosi ${\displaystyle a^{2},}$ a objętość sześcianu o tym samym boku jest równa ${\displaystyle a^{3}.}$

Dziedziną potęgowania mogą być rozmaite zbiory oraz inne klasy:

• podstawą potęgi może być element dowolnej klasy, w której określono mnożenie: liczba rzeczywista, jej uogólnienie jak liczba zespolona lub hiperzespolona, liczba kardynalna, porządkowa czy funkcja o wartościach w podanych zbiorach. W podstawie może się też znajdować macierz kwadratowa lub dowolny zbiór, ponieważ pewne działania na tych obiektach – niezwiązane wprost z arytmetyką – nazywa się odpowiednio mnożeniem macierzy oraz iloczynem kartezjańskim;
• wykładniki potęgi są już bardziej ograniczone; zawsze może nim być dodatnia liczba naturalna, a przy pewnych podstawach mogą nimi być także dowolne liczby rzeczywiste, liczby zespolone oraz kardynalne. W wykładniku może też pojawić się macierz kwadratowa^{[potrzebny przypis]} lub dowolny zbiór.

Jeśli klasy obu argumentów pokrywają się, to potęgowanie może być ściśle rozumianym działaniem dwuargumentowym, np. na zbiorze dodatnich liczb naturalnych. W tym ostatnim wypadku potęgowanie bywa uznawane za piąte działanie arytmetyczne i włączane w zakres arytmetyki elementarnej^{[potrzebny przypis]}.

Za pomocą potęgowania definiuje się inne funkcje jak pierwiastkowanie, logarytmy, wielomiany, tetracja i inne działania, które opisuje notacja strzałkowa. Między innymi przez to potęgowanie jest używane w różnych działach matematyki jak teoria liczb, kombinatoryka, algebra, geometria – zwłaszcza analityczna i algebraiczna – oraz analiza i teoria mnogości.

Etymologia

Tę sekcję należy dopracować: od 2024-03 → zweryfikować treść i dodać przypisy, od 2024-03 → poprawić tłumaczenie fragmentów tekstu/pojęć (uwaga! nie należy używać automatycznych translatorów bez sprawdzenia uzyskanego dzięki nim tłumaczenia). Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tej sekcji. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tej sekcji.

Termin „wykładnik” (ang. exponent) wywodzi się z łacińskiego „exponentem”, czasownika w formie imiesłowu teraźniejszego, od „exponere”, co oznacza „wystawiać”. Termin „potęga” (łac. potentia, potestas, dignitas. ang. power) to błędne tłumaczenie starogreckiego słowa δύναμις (dúnamis, tutaj: „wzmacnianie”), używanego przez greckiego matematyka Euklidesa do kwadratu linii, naśladując Hipokratesa z Chios^{[potrzebny przypis]}.

Definicje dla różnych przypadków

Wykładnik naturalny

Niech ${\displaystyle a\in \mathbb {R} }$ oraz ${\displaystyle n\in \mathbb {N} .}$ Potęgę ${\displaystyle a^{n}}$ definiuje się jako pomnożenie n takich samych elementów ${\displaystyle a}$ przez siebie, czyli^[2]

${\displaystyle a^{n}=\underbrace {a\cdot a\cdots a} _{n}}$

i czyta się go „${\displaystyle a}$ podniesione do ${\displaystyle n}$-tej potęgi”, „${\displaystyle a}$ do ${\displaystyle n}$-tej potęgi” lub nawet „${\displaystyle a}$ do ${\displaystyle n}$-tej”. W szczególności

${\displaystyle a^{1}=a.}$

(1)

Dodatkowo przyjmuje się

${\displaystyle a^{0}=1.}$

(3)

Z definicji potęgi wynika, iż ${\displaystyle 0^{n}=0}$ oraz ${\displaystyle 1^{n}=1}$ dla dowolnego ${\displaystyle n\in \mathbb {N} _{+}.}$

Z definicji wynika też ${\displaystyle 0^{0}=1,}$ chociaż w niektórych działach matematyki wyrażenie ${\displaystyle 0^{0}}$ jest traktowane jako niejednoznaczne (patrz oddzielna sekcja).

Potęgę naturalną można zdefiniować indukcyjnie

${\displaystyle a^{n}={\begin{cases}1&{\mbox{ dla }}n=0\\[2pt]a^{n-1}\cdot a&{\mbox{ dla }}n\geqslant 1\end{cases}}}$

Definicję tę można wprowadzić w dowolnym monoidzie z mnożeniem ${\displaystyle \cdot ;}$ może to być mnożenie liczb całkowitych, wymiernych, rzeczywistych czy zespolonych, może to być składanie funkcji określonych na zbiorze.

Dla dowolnych ${\displaystyle m,n\in \mathbb {N} }$ zachodzą własności:

• ${\displaystyle a^{m+n}=a^{m}\cdot a^{n}}$

  (2)

  Dowód:
  ${\displaystyle a^{m}\cdot a^{n}=\overbrace {\underbrace {a\cdot a\cdots a} _{m}\cdot \underbrace {a\cdot a\cdots a} _{n}} ^{m+n}}$

• ${\displaystyle (a^{m})^{n}=a^{m\cdot n}}$
  Dowód:
  ${\displaystyle (a^{m})^{n}=\overbrace {\underbrace {a\cdot a\cdots a} _{m}\cdot \underbrace {a\cdot a\cdots a} _{m}\cdots \underbrace {a\cdot a\cdots a} _{m}} ^{n}}$
  ${\displaystyle a}$ jest tu powtórzone ${\displaystyle m\cdot n}$ krotnie.

Ponadto dla grupy przemiennej:

• ${\displaystyle (a\cdot b)^{m}=a^{m}\cdot b^{m}}$
  Dowód:
  ${\displaystyle (a\cdot b)^{m}=\underbrace {(a\cdot b)\cdot (a\cdot b)\cdots (a\cdot b)} _{m}=\underbrace {a\cdot a\cdots a} _{m}\cdot \underbrace {b\cdot b\cdots b} _{m}=a^{m}\cdot b^{m}}$
  Jest tak, ponieważ gdy zamienimy mnożone liczby miejscami, to wynik się nie zmieni.

Wykładnik całkowity

Niech ${\displaystyle a\in \mathbb {R} ,a\neq 0.}$ Definicję potęgowania można rozszerzyć na wykładniki całkowite:

niech ${\displaystyle n\in \mathbb {Z} ,}$ wówczas

${\displaystyle a^{n}={\begin{cases}a^{n}&{\mbox{ dla }}n\geqslant 0\\[2pt]{\frac {1}{a^{-n}}}&{\mbox{ dla }}n<0\end{cases}}}$

Z definicji wynika, że dla ${\displaystyle n\in \mathbb {N} }$ zachodzi^[2]

${\displaystyle a^{-n}={\frac {1}{a^{n}}}}$

w szczególności

${\displaystyle a^{-1}={\frac {1}{a}}.}$

Definicję można wprowadzić w dowolnej grupie, tzn. od elementu ${\displaystyle a}$ wymaga się, aby był elementem odwracalnym.

Dla ${\displaystyle m,n\in \mathbb {Z} }$ zachodzą własności:

${\displaystyle a^{m+n}=a^{m}\cdot a^{n}.}$

${\displaystyle (a^{m})^{n}=a^{m\cdot n}.}$

(4)

Ponadto dla grupy przemiennej

${\displaystyle (a\cdot b)^{m}=a^{m}\cdot b^{m},}$

${\displaystyle \left({\frac {a}{b}}\right)^{m}={\frac {a^{m}}{b^{m}}},\qquad {}}$ gdzie ${\displaystyle {\frac {x}{y}}}$ oznacza zdefiniowane w grupie dzielenie ${\displaystyle x\cdot y^{-1}.}$

Wykładnik wymierny

Niech ${\displaystyle a\in \mathbb {R} ,a>0.}$ Definicję potęgowania można rozszerzyć na wykładniki wymierne.

Niech ${\displaystyle w\in \mathbb {Q} }$ oraz ${\displaystyle w={\frac {m}{n}},\;m,n\in \mathbb {Z} .}$

${\displaystyle a^{w}=a^{\frac {m}{n}}={\sqrt[{n}]{a^{m}}}}$

(6)

Dowód:

${\displaystyle {\sqrt[{n}]{a^{m}}}^{n}=a^{m}}$ ponieważ ${\displaystyle {\sqrt[{n}]{a^{m}}}}$ to liczba która z definicji podniesiona do n-tej daje ${\displaystyle a^{m}.}$ Natomiast ${\displaystyle a(^{\frac {m}{n}})^{n}=a^{m}}$ (patrz początek artykułu o potędze naturalnej: wynika z tego, że lewe strony obu równań są sobie równe, ponieważ podniesione do tej samej potęgi muszą dawać taki sam wynik).

W szczególności

${\displaystyle a^{\frac {1}{n}}={\sqrt[{n}]{a}}}$

W powyższych definicjach ${\displaystyle {\sqrt[{n}]{c}}}$ oznacza arytmetyczny pierwiastek z liczby dodatniej ${\displaystyle c.}$ Definicja jest poprawna i jednoznacznie określa potęgę, bowiem istnieje dokładnie jedno rozwiązanie rzeczywiste dodatnie równania ${\displaystyle x^{n}=c.}$

Dla ${\displaystyle m,n\in \mathbb {Q} ,\;a,b>0}$ zachodzą własności:

${\displaystyle a^{m+n}=a^{m}\cdot a^{n}.}$

${\displaystyle (a^{m})^{n}=a^{m\cdot n}.}$

${\displaystyle (a\cdot b)^{m}=a^{m}\cdot b^{m},}$

${\displaystyle \left({\frac {a}{b}}\right)^{m}={\frac {a^{m}}{b^{m}}}.}$

Wykładnik rzeczywisty

Dla wykładników wymiernych potęgowanie można było traktować (o ile było wykonalne) jako złożenie potęgowania naturalnego (wielokrotne mnożenie), potęgi o wykładniku -1 (odwracania elementu) i odwrotności potęgi (pierwiastkowania). Definicja potęgowania dodatniej liczby rzeczywistej o wykładniku rzeczywistym jest nieco bardziej zawiła, gdyż liczba niewymierna nie może być uzyskana tą drogą.

Wystarczy jednak w niej uwzględnić, iż liczby rzeczywiste są możliwe do uzyskania jako granice ciągów liczb wymiernych (tzw. ciągi Cauchy’ego). Na podstawie powyższych rozważań zdefiniowana jest potęga ${\displaystyle x^{y}}$ dla nieujemnych ${\displaystyle x\in \mathbb {R} ,}$ oraz ${\displaystyle y\in \mathbb {Q} .}$ Jeżeli ${\displaystyle y}$ jest liczbą niewymierną, tzn. ${\displaystyle y\in \mathbb {R} \setminus \mathbb {Q} ,}$ to wystarczy skonstruować ciąg liczb wymiernych ${\displaystyle y_{1},y_{2},\dots }$ o granicy w ${\displaystyle y}$ i przyjąć

${\displaystyle x^{y}=\lim _{n\to \infty }~x^{y_{n}}.}$

Z własności granic tak określona potęga niewymierna istnieje i spełnia żądane wcześniej własności (1–6). Potęgę rzeczywistą można też równoważnie zdefiniować jako

${\displaystyle x^{y}=\sup\{x^{p}\colon p<y{\mbox{ i }}p\in \mathbb {Q} \}.}$

W obu przypadkach korzysta się z ciągłości.

Funkcja wykładnicza

 Osobny artykuł: funkcja wykładnicza.

Jeżeli ${\displaystyle a>0,}$ to układ równań funkcyjnych (por. (1) i (2)):

${\displaystyle {\begin{cases}f_{a}(x+y)=f_{a}(x)\cdot f_{a}(y)\\f_{a}(1)=a\end{cases}}}$

definiuje jedyną (wszędzie) ciągłą^[b] funkcję ${\displaystyle f_{a}\colon \mathbb {R} \to \mathbb {R} ,}$ gdzie ${\displaystyle a\in \mathbb {R} ,}$ dla której zachodzi

${\displaystyle f_{a}(x)=a^{x}.}$

Funkcję ${\displaystyle f_{a}}$ nazywa się funkcją wykładniczą o podstawie ${\displaystyle a.}$ Z powodu dogodnych własności liczby ${\displaystyle e}$ (podstawy logarytmu naturalnego) przyjęło się definiować funkcję wykładniczą o tej podstawie, a następnie, za pomocą logarytmu naturalnego, definiuje się potęgowanie nieujemnej liczby rzeczywistej o wykładniku rzeczywistym. Jest on o tyle wygodniejszy od poprzedniej definicji, iż łatwo uogólnia się na liczby zespolone, a nawet inne struktury (np. macierze kwadratowe, zob. dalej). Funkcja (elementarna) ${\displaystyle \exp }$ może być zadana za pomocą szeregu potęgowego

${\displaystyle \exp(x)=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}},}$

który jest zbieżny dla dowolnego ${\displaystyle x\in \mathbb {R} }$ (a nawet ${\displaystyle x\in \mathbb {C} }$). Zachodzą własności (1–6), a w szczególności definiujące potęgę własności (2–3):

${\displaystyle \exp(x+y)=\exp(x)\cdot \exp(y)}$

oraz

${\displaystyle \exp(0)=1.}$

Dowodzi się również ciągłości i monotoniczności funkcji ${\displaystyle \exp }$ oraz tego, iż

${\displaystyle \exp(1)=e.}$

Mając daną funkcję wykładniczą, definiuje się funkcję logarytmu naturalnego ${\displaystyle \ln(x),}$ będącą przypadkiem szczególnym funkcji logarytmicznej, jako funkcją odwrotną do ${\displaystyle \exp(x)}$^[c] dla ${\displaystyle x\in \mathbb {R} }$ (stąd również i ona jest ciągła oraz monotoniczna). Następnie definiuje się potęgę wzorem

${\displaystyle x^{y}=\exp(y\ln(x)),}$

który czyni zadość wymaganym własnościom potęgi i jest dobrze określony dla ${\displaystyle x>0}$ oraz ${\displaystyle y\in \mathbb {R} .}$

Ujemna podstawa

Równanie ${\displaystyle x^{n}=a}$ nie ma rozwiązań rzeczywistych dla ${\displaystyle a<0}$ oraz parzystego ${\displaystyle n,}$ choć ma jedno dla ${\displaystyle n}$ nieparzystego. W oparciu o ten fakt często rozszerza się definicję pierwiastka (potęgi o wykładniku wymiernym) w następujący sposób: potęga ujemnej liczby rzeczywistej o wykładniku całkowitym jest liczbą rzeczywistą, potęgi o wykładnikach wymiernych, których mianownik jest liczbą nieparzystą, określa się za pomocą pierwiastków. Zasadniczym problemem jest fakt, iż nie istnieje liczba rzeczywista ${\displaystyle x}$ będąca rozwiązaniem równania ${\displaystyle x^{2}=-1,}$ dlatego definicja potęgi dla wykładnika będącego liczbą parzystą (licznik i mianownik są względnie pierwsze) wymaga użycia jednostki urojonej ${\displaystyle i}$ będącej jednym z rozwiązań wspomnianego równania.

Metoda korzystająca z logarytmów zawodzi, ponieważ ${\displaystyle e^{x}>0}$ dla dowolnej ${\displaystyle x\in \mathbb {R} ,}$ stąd dla ${\displaystyle a\leqslant 0}$ liczba ${\displaystyle \ln y}$ nie jest rzeczywista (z drugiej strony można zdefiniować potęgi zespolone liczb ujemnych, wybierając logarytm zespolony z ${\displaystyle y.}$

Do określenia potęgi ujemnej liczby rzeczywistej nie można również skorzystać z metody wykładnika wymiernego, gdyż opiera się ona na ciągłości. Funkcja ${\displaystyle f(x)=a^{x}}$ ma dokładnie jedno rozszerzenie ciągłe z liczb wymiernych w liczby rzeczywiste dla dowolnego ${\displaystyle a>0,}$ lecz okazuje się, że jeżeli ${\displaystyle a<0,}$ to funkcja ${\displaystyle f}$ nie jest ciągła nawet w zbiorze liczb wymiernych, w którym została określona.

Na przykład jeśli ${\displaystyle a=-1,}$ to pierwiastkiem ${\displaystyle n}$-tego stopnia z ${\displaystyle -1}$ dla każdej nieparzystej liczby naturalnej ${\displaystyle n>0}$ jest ${\displaystyle -1.}$ Niech ${\displaystyle n}$ będzie nieparzystą dodatnią liczbą całkowitą, wówczas ${\displaystyle (-1)^{m/n}=-1}$ dla ${\displaystyle m}$ nieparzystych i ${\displaystyle (-1)^{m/n}=1}$ dla ${\displaystyle m}$ parzystych. Stąd zbiór liczb wymiernych ${\displaystyle q,}$ dla których ${\displaystyle (-1)^{q}=1}$ jest gęsty w zbiorze liczb wymiernych, podobnie zbiór tych ${\displaystyle q,}$ dla których ${\displaystyle (-1)^{q}=-1,}$ co oznacza, że funkcja ${\displaystyle (-1)^{q}}$ jest nieciągła w dowolnym punkcie ${\displaystyle q}$ należącym do zbioru liczb wymiernych, w którym została zdefiniowana.

Liczby zespolone

Wykładnik zespolony

Kluczem do zrozumienia ${\displaystyle \exp(ix)}$ dla rzeczywistych wartości ${\displaystyle x}$ jest interpretacja geometryczna działań na liczbach zespolonych oraz definicja potęg liczby ${\displaystyle e,}$ czyli funkcji wykładniczej ${\displaystyle \exp .}$ Niech dany będzie na płaszczyźnie zespolonej trójkąt prostokątny o wierzchołkach ${\displaystyle (0,1,1+{\tfrac {ix}{n}}).}$ Dla dużych wartości ${\displaystyle n}$ jest nieomalże wycinkiem kołowym o rozwartości kąta środkowego równej ${\displaystyle {\tfrac {x}{n}}}$ radianów. Trójkąty ${\displaystyle (0,(1+{\tfrac {ix}{n}})^{k},(1+{\tfrac {ix}{n}})^{k+1})}$ są podobne dla wszystkich ${\displaystyle k.}$ Stąd dla dużych ${\displaystyle n}$ punkt graniczny ciągu ${\displaystyle (1+{\tfrac {ix}{n}})^{n}}$ jest punktem okręgu jednostkowego, którego kąt liczony od dodatniej osi rzeczywistej wynosi ${\displaystyle x}$ radianów. Współrzędnymi biegunowymi (postacią trygonometryczną) tego punktu są ${\displaystyle 1=(r,\theta )=(1,x),}$ a współrzędnymi prostokątnymi (postacią algebraiczną) para ${\displaystyle (\cos x,\sin x).}$ W ten sposób ${\displaystyle 1=e^{ix}=\cos x+i\sin x.}$ Zależność ta nazywana jest wzorem Eulera i łączy ona algebrę z trygonometrią poprzez liczby zespolone.

Rozwiązaniem równania ${\displaystyle e^{z}=1}$ są całkowite wielokrotności ${\displaystyle 2\pi i{:}}$

${\displaystyle \{z\colon e^{z}=1\}=\{2k\pi i\colon k\in \mathbb {Z} \}.}$

Ogólniej, jeśli ${\displaystyle e^{b}=a,}$ to każde rozwiązanie ${\displaystyle e^{z}=a}$ może być uzyskane przez dodanie całkowitej wielokrotności ${\displaystyle 2\pi i}$ do ${\displaystyle b{:}}$

${\displaystyle \{z\colon e^{z}=a\}=\{b+2k\pi i\colon k\in \mathbb {Z} \}.}$

Zespolona funkcja wykładnicza jest zatem funkcją okresową o okresie głównym ${\displaystyle 2\pi i.}$

Ostatecznie:

${\displaystyle e^{\pi i}=-1,}$

${\displaystyle e^{x+iy}=e^{x}(\cos y+i\sin y).}$

Ze wzoru Eulera wynika też, że funkcje trygonometryczne sinusa i cosinusa spełniają zależności:

${\displaystyle \cos(z)={\frac {e^{iz}+e^{-iz}}{2}}\qquad \sin(z)={\frac {e^{iz}-e^{-iz}}{2i}}.}$

Przed odkryciem liczb zespolonych funkcje sinusa i cosinusa definiowano geometrycznie, powyższe wzory upraszczają skomplikowane wzory na sumę kątów funkcji trygonometrycznych do prostego wzoru na potęgowanie:

${\displaystyle e^{i(x+y)}=e^{ix}e^{iy}.}$

W ten sposób potęgowanie wykładników zespolonych sprowadza wiele problemów trygonometrycznych do zagadnień algebraicznych.

Potęgę ${\displaystyle e^{x+iy}}$ oblicza się jako ${\displaystyle e^{x}e^{iy},}$ gdzie czynnik rzeczywisty ${\displaystyle e^{x}}$ jest modułem, zaś ${\displaystyle e^{iy}}$ to kierunek (wraz ze zwrotem, ${\displaystyle y}$ nazywany jest argumentem) liczby ${\displaystyle e^{x+iy}.}$

Potęga zespolona

Tę sekcję należy dopracować: opisać dokładniej logarytm i pierwiastki z jedynki. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tej sekcji. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tej sekcji.

Jeżeli ${\displaystyle a}$ jest dodatnią liczbą rzeczywistą, a ${\displaystyle z}$ dowolną liczbą zespoloną, to potęgę ${\displaystyle a^{z}}$ definiuje się wzorem

${\displaystyle a^{z}=e^{z\ln a},}$

gdzie ${\displaystyle x=\ln a}$ jest jedynym rozwiązaniem rzeczywistym równania ${\displaystyle e^{x}=a.}$

Jeżeli ${\displaystyle a}$ jest liczbą zespoloną, to napotyka się pewne trudności: definiuje się albo funkcje nieciągłe, albo wielowartościowe. W dziedzinie zespolonej ${\displaystyle \ln(x)}$ jest funkcją wielowartościową, a różnica między jej wartościami wynosi ${\displaystyle 2k\pi i}$ dla ${\displaystyle k\in \mathbb {Z} ,}$ to i funkcja wykładnicza jest określona niejednoznacznie, miewając nieskończoną liczbę wartości.

Niech ${\displaystyle z=\mathrm {Ln} (x)}$ będzie dowolnie wybraną gałęzią logarytmu ${\displaystyle x,}$ wówczas:

${\displaystyle x^{y}=e^{y(z+2k\pi i)}=e^{yz}e^{y2k\pi i},}$

czyli moduł ${\displaystyle x^{y}}$ wynosi wtedy ${\displaystyle \exp(y\mathrm {Ln} (x))\in \mathbb {R} ,}$ zaś jej argument przyjmuje dowolną z wartości ${\displaystyle 2k\pi y.}$ Potęga będzie miała ${\displaystyle n}$ wartości tylko wtedy, gdy ${\displaystyle y=c/n,}$ gdzie ${\displaystyle c}$ i ${\displaystyle n}$ są względnie pierwsze). Jeżeli ${\displaystyle y\in \mathbb {Z} ,}$ to wygodnie jest korzystać ze wzoru de Moivre’a.

Należy tylko pamiętać o dziedzinie potęgowania, przypadku szczególnym ${\displaystyle 0^{0}}$ i o wieloznaczności potęgowania w liczbach zespolonych. Nieuwzględnienie tych warunków i branie pierwiastka arytmetycznego może doprowadzić do sprzeczności, np.

${\displaystyle ((-1)^{2})^{\tfrac {1}{2}}=1\neq -1=(-1)^{2\cdot {\tfrac {1}{2}}}.}$

Funkcja potęgowa

 Osobny artykuł: funkcja potęgowa.

Funkcja wykładnicza zdefiniowana jest przez potęgowanie, gdzie zmienną jest wykładnik, a podstawa jest stałą. Sytuacja odwrotna, w której ustalony jest wykładnik, a podstawa jest zmienna, również jest funkcją potęgową, co można było zaobserwować wyżej (wzór (5)). Określenie funkcji pierwiastkowej, czyli funkcji potęgowej o wykładniku będącym odwrotnością niezerowej liczby całkowitej przebiega identycznie jak wyżej. Problemem znowu staje się zdefiniowanie funkcji o wykładniku niewymiernym, jednak pokonuje się ją analogicznie i dowodzi się wielu jej własności (ciągłość, monotoniczność na przedziałach).

Własności

Tę sekcję należy dopracować: opisać dokładnie założenia poszczególnych własności. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tej sekcji. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tej sekcji.

Potęgowanie nie jest działaniem przemiennym, np. ${\displaystyle 8=2^{3}\neq 3^{2}=9.}$ Nie jest także łączne, np. ${\displaystyle 2^{(3^{2})}=2^{9}=512,}$ lecz ${\displaystyle {(2^{3})}^{2}=8^{2}=64.}$

Złożone potęgowanie, zgodnie z regułami kolejności wykonywania działań, traktuje się jako prawostronnie łączne, np. ${\displaystyle 2^{3^{2}}=2^{(3^{2})}.}$

Istnienie dwóch funkcji zawierających potęgę jako argument i dwóch funkcji odwrotnych wynika właśnie z nieprzemienności potęgowania. Zachodzą następujące wzory^[2]:

• ${\displaystyle a^{r+s}=a^{r}\cdot a^{s},}$
• ${\displaystyle (a^{r})^{s}=a^{r\cdot s}.}$

Jeżeli mnożenie jest przemienne, to zachodzi również^[2]

• ${\displaystyle (a\cdot b)^{r}=a^{r}\cdot b^{r}.}$

Jeżeli ${\displaystyle a^{s}}$ jest elementem odwracalnym, to^[2]

• ${\displaystyle a^{r-s}={\frac {a^{r}}{a^{s}}}.}$

Dla ${\displaystyle r=0}$ powyższy wzór oznacza:

• ${\displaystyle a^{-s}={\frac {1}{a^{s}}}.}$

Jeżeli tak ${\displaystyle b,}$ jak i ${\displaystyle b^{r}}$ są odwracalne, to^[2]

• ${\displaystyle \left({\frac {a}{b}}\right)^{r}={\frac {a^{r}}{b^{r}}}.}$

Zero do potęgi zerowej

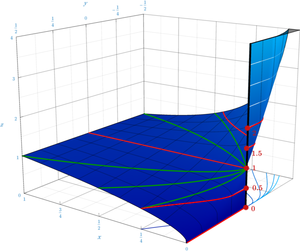
Większość autorów zgadza się z zamieszczonymi w poniższych listach stwierdzeniami dotyczącymi ${\displaystyle 0^{0},}$ lecz dochodzą do różnych wniosków, czy definiować wyrażenie ${\displaystyle 0^{0},}$ czy też nie (zob. następną podsekcję).

W większości przypadków, które nie wykorzystują ciągłości (na przykład ograniczając się wyłącznie do wykładników całkowitych) interpretowanie ${\displaystyle 0^{0}}$ jako ${\displaystyle 1}$ upraszcza wzory i eliminuje konieczność rozważania przypadków szczególnych w twierdzeniach (por. przypadki niżej, które wykorzystują ciągłość). Na przykład:

• postrzeganie ${\displaystyle 0^{0}}$ jako iloczynu pustego zer sugeruje wartość równą ${\displaystyle 1;}$
• interpretacją kombinatoryczną ${\displaystyle 0^{0}}$ jest liczba pustych krotek elementów zbioru pustego: istnieje dokładnie jedna pusta krotka;
• równoważnie interpretacją teoriomnogościową ${\displaystyle 0^{0}}$ jest liczba funkcji ze zbioru pustego w zbiór pusty: istnieje dokładnie jedna taka funkcja – funkcja pusta^[3];
• znacząco upraszcza teorię wielomianów i szeregów potęgowych dzięki temu, iż wyraz wolny może być zapisany jako ${\displaystyle ax^{0}}$ dla dowolnego ${\displaystyle x,}$ np.
  • wzór na współczynniki iloczynu wielomianów straciłby na prostocie, gdyby wyrazy wolne musiałyby być traktowane oddzielnie;
  • dla dzielników zera (elementów pierścieni spełniających ${\displaystyle a,b\neq 0,}$ ale ${\displaystyle ab=0}$) z własności potęgowania otrzymuje się ${\displaystyle 1=a^{0}b^{0}=(ab)^{0}=0^{0};}$
  • tożsamości postaci ${\displaystyle \textstyle {\tfrac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}}$ i ${\displaystyle \textstyle e^{x}=\sum _{n=0}^{\infty }{\tfrac {x^{n}}{n!}}}$ nie są poprawne dla ${\displaystyle x=0,}$ jeśli ${\displaystyle 0^{0}\neq 1.}$
  • twierdzenie o dwumianie ${\displaystyle \textstyle (1+x)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{k}}$ nie jest poprawne dla ${\displaystyle x=0,}$ jeżeli ${\displaystyle 0^{0}\neq 1}$^[4];
• w rachunku różniczkowym wzór na różniczkę jednomianu ${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} x}}x^{n}=nx^{n-1}}$ nie jest poprawny dla ${\displaystyle n=1}$ w punkcie ${\displaystyle x=0,}$ gdy ${\displaystyle 0^{0}\neq 1.}$

Z drugiej strony ${\displaystyle 0^{0}}$ musi być uważane za wyrażenie nieoznaczone w kontekstach, gdzie wykładnik zmienia się w sposób ciągły:

• jeżeli ${\displaystyle f(t)}$ i ${\displaystyle g(t)}$ są funkcjami o wartościach rzeczywistych zbiegającymi do ${\displaystyle 0}$ (gdy ${\displaystyle t}$ zbiega do liczby rzeczywistej bądź ${\displaystyle \pm \infty }$), gdzie ${\displaystyle f(t)>0,}$ to funkcja ${\displaystyle f(t)^{g(t)}}$ nie musi zbiegać do ${\displaystyle 1.}$ Rzeczywiście, w zależności od ${\displaystyle f}$ i ${\displaystyle g}$ granica ${\displaystyle f(t)^{g(t)}}$ może być dowolną nieujemną liczbą rzeczywistą bądź ${\displaystyle +\infty }$ albo może być nieokreślona. Granice zawierające operacje algebraiczne mogą być często wyznaczone przez zamianę podwyrażeń ich granicami; jeśli wyrażenie wynikowe nie określa oryginalnej granicy, to wyrażenie nazywa się nieoznaczonym (ma postać nieoznaczoną)^[5]

Przykładowo funkcje niżej są postaci ${\displaystyle f(t)^{g(t)},}$ gdzie ${\displaystyle f(t),g(t)\to 0}$ dla ${\displaystyle t\to 0^{+}}$ (zob. granica jednostronna), ale ich granice nie są równe:

${\displaystyle \lim _{t\to 0^{+}}t^{t}=1,\quad \lim _{t\to 0^{+}}(e^{-1/t^{2}})^{t}=0,\quad \lim _{t\to 0^{+}}(e^{-1/t^{2}})^{-t}=+\infty ,\quad \lim _{t\to 0^{+}}(e^{-1/t})^{at}=e^{-a}.}$

Tak więc ${\displaystyle 0^{0}}$ jest wyrażeniem nieoznaczonym. Takie zachowanie pokazuje, że funkcja ${\displaystyle x^{y}}$ dwóch zmiennych choć jest ciągłą na zbiorze ${\displaystyle \{(x,y)\colon x>0\},}$ nie może być rozszerzona do funkcji ciągłej na dowolnym zbiorze zawierającym ${\displaystyle (0,0),}$ nie ważne jak zdefiniuje się ${\displaystyle 0^{0}}$^[6].

• Funkcja ${\displaystyle z^{z}}$ jest określona dla niezerowych liczb zespolonych ${\displaystyle z}$ przez wybranie gałęzi ${\displaystyle \log z}$ i przyjęcie ${\displaystyle z^{z}:=e^{z\log z},}$ ponieważ nie ma gałęzi ${\displaystyle \log z}$ zdefiniowanej w ${\displaystyle z=0,}$ tylko w otoczeniu zera^[7]. Nie istnieje funkcja holomorficzna określona w otoczeniu zera, która byłaby zgodna z ${\displaystyle z^{z}}$ dla wszystkich dodatnich liczb rzeczywistych ${\displaystyle z.}$

Historia różnych punktów widzenia

Różni autorzy interpretują powyższą sytuację na różne sposoby:

• Niektórzy argumentują, że najlepsza wartość ${\displaystyle 0^{0}}$ zależy od kontekstu, przez co zdefiniowanie jej raz na zawsze jest problematyczne^[8]. Zgodnie z przekonaniami Bensona (1999), „The choice whether to define ${\displaystyle 0^{0}}$ is based on convenience, not on correctness.”^[9] (Wybór czy definiować ${\displaystyle 0^{0}}$ jest podyktowany wygodą, a nie poprawnością).
• Inni twierdzą, że ${\displaystyle 0^{0}}$ jest równe ${\displaystyle 1.}$ Zgodnie ze s. 408 pracy Knutha (1992), „[it] has to be ${\displaystyle 1}$” (musi być równa ${\displaystyle 1}$), choć kontynuuje on: „Cauchy had good reason to consider ${\displaystyle 0^{0}}$ as an undefined limiting form” (Cauchy miał dobry powód, by uważać ${\displaystyle 0^{0}}$ za nieokreśloną postać graniczną) oraz „in this much stronger sense, the value of ${\displaystyle 0^{0}}$ is less defined than, say, the value of ${\displaystyle 0+0}$” (w tym dużo silniejszym sensie wartość ${\displaystyle 0^{0}}$ jest słabiej określona, niż powiedzmy wartość ${\displaystyle 0+0}$; wyróżnienia oryginalne)^[10]

Debata trwa od przynajmniej początków XVII wieku. Wówczas większość matematyków zgadzała się z tym, że ${\displaystyle 0^{0}=1,}$ jednak w 1821 Cauchy^[11] umieścił ${\displaystyle 0^{0}}$ wraz z wyrażeniami postaci ${\displaystyle {\tfrac {0}{0}}}$ w tablicy wyrażeń nieoznaczonych. W latach 30. XIX wieku Libri^[12][13] opublikował nieprzekonujący dowód, iż ${\displaystyle 0^{0}=1,}$ w czym wsparł go Möbius^[14] błędnie twierdząc, że ${\displaystyle \lim _{t\to 0^{+}}f(t)^{g(t)}=1,}$ jeżeli ${\displaystyle \lim _{t\to 0^{+}}f(t)=\lim _{t\to 0^{+}}g(t)=0.}$ Komentator, który podpisał się wyłącznie literą „S” podał kontrprzykład ${\displaystyle (e^{-1/t})^{t}}$ (który może być uzyskany z jednego z powyższych przykładów, przyjmując ${\displaystyle a=1}$), który uciszył na jakiś czas debatę z oczywistym wnioskiem, iż ${\displaystyle 0^{0}}$ nie powinno być definiowane. Więcej szczegółów można znaleźć w pracy Knutha (1992)^[10].

Języki programowania i kalkulatory

Wśród języków programowania komputerów, które przypisują ${\displaystyle 0^{0}}$ wartość ${\displaystyle 1}$^[15], można wymienić bc, Common Lisp, Haskell, J, Java, JavaScript, LISP, MATLAB, ML, Perl, PHP, Python, R, Ruby, Scheme czy SQL. W .NET Framework metoda System.Math.Pow traktuje ${\displaystyle 0^{0}}$ jak ${\displaystyle 1.}$

Wśród aplikacji arkuszy kalkulacyjnych Microsoft Excel generuje błąd przy próbie wyznaczenia ${\displaystyle 0^{0},}$ podczas gdy OpenOffice.org w wersji 3 zwraca ${\displaystyle 1.}$ Google Docs Spreadsheet również zwraca ${\displaystyle 1.}$

Kalkulator systemu Microsoft Windows, Wyszukiwarka Google^[16], Derive oraz PARI/GP obliczają ${\displaystyle 0^{0}}$ równe ${\displaystyle 1.}$

Maple upraszcza ${\displaystyle a^{0}}$ do ${\displaystyle 1,}$ zaś ${\displaystyle 0^{a}}$ do ${\displaystyle 0}$ nawet, gdy nie nałożono żadnych ograniczeń na ${\displaystyle a}$ (uproszczenia te są poprawne tylko dla ${\displaystyle a\neq 0}$), z kolei ${\displaystyle 0^{0}}$ ma wartość ${\displaystyle 1.}$

Mathematica upraszcza ${\displaystyle a^{0}}$ do ${\displaystyle 1}$ nawet, gdy brak ograniczeń dla ${\displaystyle a.}$ Nie upraszcza jednak ${\displaystyle 0^{a}}$ i przyjmuje, iż ${\displaystyle 0^{0}}$ jest symbolem nieoznaczonym.

Sage upraszcza ${\displaystyle a^{0}}$ do ${\displaystyle 1}$ nawet, jeżeli nie ograniczono w żaden sposób ${\displaystyle a.}$ Nie upraszcza ${\displaystyle 0^{a}}$ i przyjmuje, że ${\displaystyle 0^{0}}$ ma wartość ${\displaystyle 1.}$

Kalkulatory TI-83 Plus i TI-84 zwracają błąd dziedziny (Domain Error) podczas rozwiązywania ${\displaystyle 0^{0},}$ lecz TI-89 zwraca ${\displaystyle 1.}$ TI-89 Titanium zwraca wartość undef.

Notacja

Jak wspomniano na początku, potęgowanie zapisuje się zwykle, umieszczając wykładnik w indeksie górnym za podstawą, np. ${\displaystyle x^{y}.}$ Gdy jednak ze względów technicznych nie można użyć indeksu górnego stosuje się często zapisy ${\displaystyle x{\hat {\ }}y,}$ ${\displaystyle x**y}$ lub ${\displaystyle x\uparrow y.}$

W przypadku, gdy podstawą potęgi jest liczba ${\displaystyle e}$ (podstawa logarytmu naturalnego), to zamiast zapisu ${\displaystyle e^{x}}$ stosuje się często zapis ${\displaystyle \exp(x)}$ (pomijając niekiedy nawiasy), gdyż dla liczb rzeczywistych potęgi liczby ${\displaystyle e}$ pokrywają się z wartościami funkcji ${\displaystyle \exp .}$

Funkcje

Choć zapis ${\displaystyle f^{n}(x)}$ dla ${\displaystyle n\in \mathbb {N} }$ może oznaczać ${\displaystyle (f(x))^{n},}$ czyli potęgę obrazu (patrz niżej), to jednak jeśli przeciwdziedzina funkcji zawiera się w jej dziedzinie, to zapis ${\displaystyle f^{n}(x)}$ oznacza zwykle ${\displaystyle n}$-krotne złożenie funkcji samej ze sobą, czyli jej ${\displaystyle n}$-tą iterację, tzn.

${\displaystyle f^{3}=f\circ f\circ f}$

lub dokładniej

${\displaystyle f^{3}(x)=f(f(f(x))).}$

Wtedy w szczególności, ${\displaystyle f^{-1}}$ oznacza funkcję odwrotną do funkcji ${\displaystyle f,}$ oznaczeniem tym zapisuje się również przeciwobraz funkcji. Ujemny, różny od -1, indeks górny oznacza już zwykle potęgę obrazu.

W przypadku funkcji trygonometrycznych i hiperbolicznych przyjęła się konwencja według której ${\displaystyle \sin ^{n}x}$ oznacza ${\displaystyle (\sin x)^{n}}$ dla ${\displaystyle n>0}$ oraz ${\displaystyle \sin ^{-1}x=\arcsin x.}$ Podobna umowa obowiązuje w przypadku logarytmu: ${\displaystyle \log ^{3}(x)=(\log x)^{3}.}$

Z kolei podobny zapis ${\displaystyle f^{(n)}(x)}$ oznacza najczęściej ${\displaystyle n}$-tą pochodną funkcji.

Programowanie

Niżej znajdują się oznaczenia potęgowania stosowane w niektórych językach programowania:

• x ↑ y: Algol, Commodore BASIC
• x ^ y: BASIC, J, Matlab, Microsoft Excel, większość systemów Computer Algebra System (TeX, jak większość jego rozszerzeń, używa tego oznaczenia dla indeksu górnego ${\displaystyle x^{y}}$)
• x ** y: Ada, Fortran, FoxPro, Perl, Python, Ruby, SAS
• x * y: APL
• Power(x, y): Microsoft Excel
• pow(x, y): C, C++, PHP
• Math.pow(x, y): Java, JavaScript, Modula-3
• Math.Pow(x, y): C#
• (expt x y): Common Lisp, Scheme
• GLib.Math.pow(x, y) (skracane do Math.pow(x, y)): Vala

Choć w języku (Turbo) Pascal nie ma standardowej funkcji potęgowania, można ją zdefiniować następująco:

function power(x, y : real) : real;
begin
   power := exp(ln(abs(x))*y);
end;

Uogólnienia

Macierze

 Osobne artykuły: potęgowanie macierzy i eksponenta macierzy.

Potęgę naturalną, a nawet całkowitą, łatwo zdefiniować dla macierzy kwadratowych, naśladując powyższe obserwacje: jest to wielokrotne mnożenie dla wykładników dodatnich i odwracanie dla wykładników ujemnych. Podniesienie dowolnej macierzy do potęgi zerowej to zgodnie z oczekiwaniami macierz jednostkowa.

Dla macierzy kwadratowych można określić funkcję ${\displaystyle \exp }$ wzorem

${\displaystyle \exp \mathbf {A} =\sum _{k=0}^{\infty }{\frac {\mathbf {A} ^{k}}{k!}}.}$

Tak jak dla liczby rzeczywistych czy zespolonych, szereg ten jest zawsze zbieżny. Obliczanie funkcji wykładniczej macierzy ma zastosowanie przy rozwiązywaniu równań różniczkowych liniowych.

Dla macierzy diagonalnych wystarczy obliczyć wartości ${\displaystyle \exp x}$ na przekątnej: jeżeli

${\displaystyle \mathbf {A} ={\begin{bmatrix}a_{1}&0&\ldots &0\\0&a_{2}&\ldots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\ldots &a_{n}\end{bmatrix}},}$

to

${\displaystyle \exp \mathbf {A} ={\begin{bmatrix}e^{a_{1}}&0&\ldots &0\\0&e^{a_{2}}&\ldots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\ldots &e^{a_{n}}\end{bmatrix}}.}$

Jeżeli ${\displaystyle \mathbf {A} =\mathbf {UDU} ^{-1}}$ i ${\displaystyle \mathbf {D} }$ jest diagonalna, to:

${\displaystyle \exp \mathbf {A} =\mathbf {U} \exp(\mathbf {D} )\mathbf {U} ^{-1}}$

Dla macierzy nilpotentnej ${\displaystyle \mathbf {N} }$ wartość ${\displaystyle \exp \mathbf {N} }$ można obliczyć bezpośrednio z rozwinięcia na szereg potęgowy, gdyż zawiera on tylko skończenie wiele wyrazów:

${\displaystyle \exp \mathbf {N} =\mathbf {I} +\mathbf {N} +{\tfrac {1}{2!}}\mathbf {N} ^{2}+{\tfrac {1}{3!}}\mathbf {N} ^{3}+\ldots +{\tfrac {1}{(q-1)!}}\mathbf {N} ^{q-1},}$

jeśli ${\displaystyle \forall _{k\geqslant q}\;\mathbf {N} ^{k}=\mathbf {0} .}$

Zbiory i liczby kardynalne

Zapis ${\displaystyle A^{n},}$ gdzie ${\displaystyle A}$ jest zbiorem, a ${\displaystyle n}$ liczbą naturalną oznacza najczęściej ${\displaystyle n}$-krotny iloczyn kartezjański zbioru ${\displaystyle A.}$

Zapis ${\displaystyle A^{B},}$ gdzie ${\displaystyle A}$ i ${\displaystyle B}$ są zbiorami, oznacza zbiór wszystkich funkcji ${\displaystyle f}$ o dziedzinie ${\displaystyle B}$ i przeciwdziedzinie ${\displaystyle A.}$ Zastępując zbiory ich mocami, otrzymuje się definicje potęgowania liczb kardynalnych.

Wielokrotne potęgowanie

 Osobny artykuł: notacja strzałkowa.

Zastosowania

Tę sekcję należy dopracować: Sekcja wymaga poszerzenia. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tej sekcji. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tej sekcji.

Potęgi liczby 10 to liczby kończące się pewną liczbą zer. Dla skrócenia ich zapisu stosuje się tzw. przedrostki układu SI, w szczególności w notacji naukowej do zapisywania wielkich liczb i wielkości fizycznych.

Z racji konstrukcji współczesnych komputerów w informatyce często spotyka się potęgi liczby 2. Na przykład ${\displaystyle 2^{n}}$ jest liczbą możliwych wartości zmiennej składającej się z ${\displaystyle n}$ bitów (każdy bit może mieć wartość 0 lub 1, razem jest ich ${\displaystyle n}$). Z tego powodu zwykle operuje się też wielokrotnościami liczby 2 (bądź jej pewnej potęgi). Osiem bitów tworzy oktet (lub bajt), szesnaście – słowo. Większe wartości również są wielokrotnościami liczby 2, nie zaś 10, jak wskazywałyby ich nazwy, np. kilobajt to 1 024, a nie 1 000 bajtów (Dla odróżnienia tych wielkości opracowano tzw. przedrostki dwójkowe).

Funkcji wykładnicza ${\displaystyle \exp ,}$ czyli funkcja wykładnicza o podstawie ${\displaystyle e,}$ jest szeroko stosowana w matematyce, pojawiając się szczególnie często w analizie matematycznej czy rachunku prawdopodobieństwa.

Potęgowanie modulo jest używane w kryptografii, np. w algorytmie RSA.

Algorytmika

Złożoność obliczeniowa naiwnego algorytmu potęgowania (zob. wzór po (2)) wynosi ${\displaystyle \operatorname {O} (n).}$ Istnieje znacznie szybszy algorytm, nazywany algorytmem szybkiego potęgowania, korzystający z metody dziel i zwyciężaj, którego złożoność obliczeniowa jest rzędu ${\displaystyle \operatorname {O} (\log n).}$

Historia

Współczesny symbol potęgowania został wprowadzony przez Kartezjusza w dziele Geometria^[17]. Oprócz współczesnej notacji Kartezjusz używał także zapisu wykładnika dokładnie nad wyrażeniem, które podnosił do potęgi^[17].

Dawniej stosowano nazwy potęg oparte na kwadracie i sześcianie^[18]:

 Ta sekcja jest niekompletna. Jeśli możesz, rozbuduj ją.

Zobacz też

Zobacz hasło potęgowanie w Wikisłowniku

• funkcja W Lamberta

Uwagi

Przypisy

Linki zewnętrzne

Polskojęzyczne

• Tomasz Miller, Potęgowanie i „najpiękniejszy wzór matematyki” | Zacznijmy od zera #4, kanał Centrum Kopernika Badań Interdyscyplinarnych na YouTube, 23 listopada 2021 [dostęp 2023-11-26].

Anglojęzyczne

• Eric W.E.W. Weisstein Eric W.E.W., Power, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2024-02-02].
• Eric W.E.W. Weisstein Eric W.E.W., Exponent Laws, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2024-02-02].
• Eric W.E.W. Weisstein Eric W.E.W., Complex Exponentiation, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2024-02-02].
• Power (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2024-02-02].