Loi de Holtsmark

Loi de Holtsmark
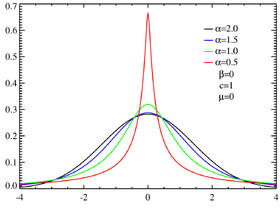Densité de probabilité densités de lois α-stables symétriques ; α=1,5 (courbe bleue) est la densité de la loi de Holtsmark
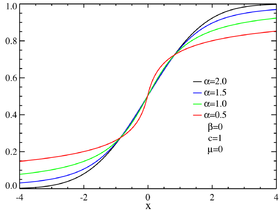Fonction de répartition fonctions de répartition de lois α-stables symétriques ; α=3/2 est celle de la loi de Holtsmark
Paramètres	${\displaystyle c\in ]0,\infty [}$ — paramètre d'échelle ${\displaystyle \mu \in ]-\infty ,\infty [}$ — paramètre de position
Support	${\displaystyle x\in \mathbb {R} }$
Densité de probabilité	voir l'article
Espérance	${\displaystyle \mu }$
Médiane	${\displaystyle \mu }$
Mode	${\displaystyle \mu }$
Variance	infinie
Asymétrie	non définie
Kurtosis normalisé	non défini
Fonction génératrice des moments	non définie
Fonction caractéristique	${\displaystyle \exp \left[{\rm {i}}t\mu \!-\!|ct|^{3/2}\right]}$
modifier

En théorie des probabilités et en statistique, la loi de Holtsmark est une loi de probabilité à densité. La loi de Holtsmark est un cas particulier de loi stable avec un indice de stabilité ${\displaystyle \alpha }$ égal à 3/2 et avec un paramètre d'asymétrie nul : ${\displaystyle \beta =0}$. Puisque ${\displaystyle \beta }$ est nul, la loi est symétrique et ainsi est un exemple de loi stable symétrique. La loi de Holtsmark est une des quelques lois stables pour lesquelles une forme explicite de la densité de probabilité est connue. Cette expression de la densité utilise des fonctions hypergéométriques.

La loi de Holtsmark est utilisée dans la physique des plasmas et en astrophysique^[1]. En 1919, le physicien norvégien Johan Peter Holtsmark propose cette loi comme modèle pour la fluctuation des champs de plasma dus au mouvement chaotique des particules^[2]. Elle s'applique également pour d'autres types de forces de Coulomb, en particulier pour modéliser la gravitation des corps, ceci montre son importance en astrophysique^[3],[4].

Fonction caractéristique

La fonction caractéristique d'une loi stable symétrique est :

${\displaystyle \varphi (t;\mu ,c)=\exp \left[{\rm {i}}t\mu \!-\!|ct|^{\alpha }\right],}$

où ${\displaystyle \alpha }$ est un paramètre de forme, ou indice de stabilité, ${\displaystyle \mu }$ est un paramètre de position, et ${\displaystyle c}$ est un paramètre d'échelle.

Puisque la loi de Holtsmark est telle que ${\displaystyle \alpha =3/2}$, sa fonction caractéristique est donnée par^[5] :

${\displaystyle \varphi (t;\mu ,c)=\exp \left[{\rm {i}}t\mu \!-\!|ct|^{3/2}\right].}$

La loi de Holtsmark est une loi stable avec ${\displaystyle \alpha >1}$ et ${\displaystyle \mu }$ est sa moyenne^[6],[7]. Puisque ${\displaystyle \beta =0}$, ${\displaystyle \mu }$ est également sa médiane et son mode. Le fait que ${\displaystyle \alpha <2}$ assure que la variance est infinie^[6]. Tous les autres moments d'ordre supérieur sont également infinis^[6]. Comme d'autres lois stables autres que la loi normale, une variance infinie indique que la dispersion de la loi est donnée par le paramètre d'échelle ${\displaystyle c}$. La dispersion de la loi peut également être décrite par les moments fractionnels^[6].

Densité de probabilité

En général la densité de probabilité ${\displaystyle f}$ d'une loi de probabilité continue peut être obtenue à partir de la fonction caractéristique par la formule :

${\displaystyle f(x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\varphi (t){\rm {e}}^{-{\rm {i}}xt}\,{\rm {d}}t.}$

La plupart des lois stables n'ont pas de forme explicite pour leur densité de probabilité. Seulement la loi normale, la loi de Cauchy et les lois de Lévy en ont en termes de fonctions élémentaires^[1]. La loi de Holtsmark est l'une des deux lois stables symétrique qui ont une densité explicite à l'aide des fonctions hypergéométriques^[1]. Lorsque ${\displaystyle \mu =0}$ et ${\displaystyle c=1}$, la densité de probabilité de la loi de Holtsmark est donnée par :

${\displaystyle {\begin{aligned}f(x;0,1)&={1 \over \pi }{\Gamma (5/3)}\ {}_{2}F_{3}(5/12,11/12;1/3,1/2,5/6;-4x^{6}/729)\\&{}\quad {}-{x^{2} \over 3\pi }\ {}_{3}F_{4}(3/4,1,5/4;2/3,5/6,7/6,4/3;-4x^{6}/729)\\&{}\quad {}+{7x^{4} \over 81\pi }{\Gamma (4/3)}\ {}_{2}F_{3}(13/12,19/12;7/6,3/2,5/3;-4x^{6}/729),\end{aligned}}}$

où ${\displaystyle \Gamma }$ est la fonction gamma et ${\displaystyle \;_{m}F_{n}}$ est une fonction hypergéométrique^[1]. On a aussi^[8]

${\displaystyle {\begin{aligned}f(x;0,1)&={\frac {-\beta ^{2}}{6\pi }}\left[~_{2}F_{2}\left(1,{\frac {3}{2}};{\frac {4}{3}},{\frac {5}{3}};-{\frac {4{\rm {i}}\beta ^{3}}{27}}\right)+~_{2}F_{2}\left(1,{\frac {3}{2}};{\frac {4}{3}},{\frac {5}{3}};{\frac {4{\rm {i}}\beta ^{3}}{27}}\right)\right]\\&+{\frac {4}{3\times 3^{2/3}}}\left[\mathrm {Bi} '\left(-{\frac {\beta ^{2}}{3\times 3^{1/3}}}\right)\cos \left({\frac {2\beta ^{3}}{27}}\right)+{\frac {\beta }{3^{2/3}}}~\mathrm {Bi} \left(-{\frac {\beta ^{2}}{3\times 3^{1/3}}}\right)\sin \left({\frac {2\beta ^{3}}{27}}\right)\right],\end{aligned}}}$

où ${\displaystyle \mathrm {Bi} }$ est la fonction d'Airy du deuxième type et ${\displaystyle \mathrm {Bi} '}$ sa dérivée. Les arguments des fonctions hypergéométriques ${\displaystyle _{2}F_{2}}$ sont des nombres complexes imaginaires purs opposés, mais la somme des deux fonctions est réelle. Pour ${\displaystyle x}$ positif, la fonction ${\displaystyle \mathrm {Bi} (-x)}$ est reliée aux fonctions de Bessel d'ordre fractionnaire ${\displaystyle J_{-1/3}}$ et ${\displaystyle J_{1/3}}$ et sa dérivée aux fonctions de Bessel d'ordre fractionnaire ${\displaystyle J_{-2/3}}$ et ${\displaystyle J_{2/3}}$. On peut ainsi écrire^[8]

${\displaystyle {\begin{aligned}f(x;0,1)&={\frac {4\beta ^{2}}{27{\sqrt {3}}}}\left\{\cos \left({\frac {2\beta ^{3}}{27}}\right)\left[J_{-2/3}\left({\frac {2\beta ^{3}}{27}}\right)+J_{2/3}\left({\frac {2\beta ^{3}}{27}}\right)\right]+\sin \left({\frac {2\beta ^{3}}{27}}\right)\left[J_{-1/3}\left({\frac {2\beta ^{3}}{27}}\right)-J_{1/3}\left({\frac {2\beta ^{3}}{27}}\right)\right]\right\}\\&-{\frac {\beta ^{2}}{6\pi }}\left[~_{2}F_{2}\left(1,{\frac {3}{2}};{\frac {4}{3}},{\frac {5}{3}};-{\frac {4{\rm {i}}\beta ^{3}}{27}}\right)+~_{2}F_{2}\left(1,{\frac {3}{2}};{\frac {4}{3}},{\frac {5}{3}};{\frac {4{\rm {i}}\beta ^{3}}{27}}\right)\right].\end{aligned}}}$

Références

• Portail des probabilités et de la statistique