Phân phối Poisson

Phân phối Poisson

Hàm khối xác suất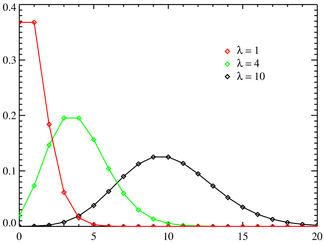 Trục hoành là chỉ số k. Hàm khối xác suất được định nghĩa dựa trên duy nhất biến nguyên k. Đường nối dùng để minh họa chứ không có nghĩa là liên tục.
Hàm phân phối tích lũy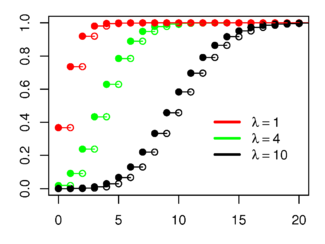 Trục hoành là chỉ số k.
Tham số	${\displaystyle \lambda \in (0,\infty )}$
Giá	${\displaystyle k\in \{0,1,2,\ldots \}}$
Hàm khối xác suất	${\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}\!}$
Hàm phân phối tích lũy	${\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}}\!{\text{ for }}k\geq 0}$ (với ${\displaystyle \Gamma (x,y)}$ là hàm gamma không đầy đủ)
Giá trị kỳ vọng	${\displaystyle \lambda \,}$
Trung vị	${\displaystyle {\text{usually about }}\lfloor \lambda +1/3-0.02/\lambda \rfloor }$
Yếu vị	${\displaystyle \lceil \lambda \rceil -1}$
Phương sai	${\displaystyle \lambda \,}$
Độ xiên	${\displaystyle \lambda ^{-1/2}\,}$
Độ nhọn	${\displaystyle \lambda ^{-1}\,}$
Entropy	${\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}$
Hàm sinh mô men	${\displaystyle \exp(\lambda (e^{t}-1))\,}$
Hàm đặc trưng	${\displaystyle \exp(\lambda (e^{it}-1))\,}$

Trong lý thuyết xác suất và thống kê, Phân phối Poisson (Tiếng Anh: Poisson distribution) là một phân phối xác suất rời rạc cho biết xác suất xảy ra một số lượng sự kiện trong một khoảng thời gian nhất định không đổi và với một tỷ lệ trung bình cho trước. Tỷ lệ trung bình đó được ký hiệu là ${\displaystyle \lambda }$.

Phân phối Poisson còn được dùng cho khoảng mà đơn vị khác thời gian như: khoảng cách, diện tích hay thể tích. Một ví dụ cổ điển là sự phân rã hạt nhân của các nguyên tử.

Phân phối này được tìm ra bởi nhà toán học Siméon-Denis Poisson (1781–1840) và đã được xuất bản cùng với lý thuyết xác suất của ông, vào năm 1838 với tựa đề Recherches sur la probabilité des jugements en matières criminelles et matière civile ("Research on the Probability of Judgments in Criminal and Civil Matters"). Theo đó, nếu xem xét một biến ngẫu nhiên N nào đó, và đếm số lần xuất hiện (rời rạc) của nó trong một khoảng thời gian cho trước. Nếu giá trị kì vọng (hay số lần trung bình mà biến ngẫu nhiên đó xảy ra trong khoảng thời gian đó là λ, thì xác suất để cũng chính sự kiện đó xảy ra k lần (k là số nguyên không âm, k = 0, 1, 2,...) sẽ được tính theo công thức

${\displaystyle f(k;\lambda )={\frac {\lambda ^{k}e^{-\lambda }}{k!}},\,\!}$

với

• e là cơ số của logarit tự nhiên (e = 2.71828...)
• k là số lần xuất hiện của một sự kiện - mà xác suất của nó là cho bởi công thức trên
• k! là giai thừa của k
• λ là số thực dương, bằng với giá trị kì vọng xuất hiện của sự kiện trong một khoảng cho sẵn. Ví dụ, nếu một sự kiện trung bình xảy ra 1 lần trong 4 phút, giờ ta quan tâm số lần sự kiện xảy ra trong khoảng thời gian 10 phút, ta dùng mô hình phân phối Poisson với λ = 10/4 = 2.5.

Vì đây là biến ngẫu nhiên rời rạc, công thức trên cho ta công thức của hàm khối xác suất.

${\displaystyle p_{X}[k]={\frac {\lambda ^{k}e^{-\lambda }}{k!}}\,\!}$

Các phân phối liên quan

• Nếu ${\displaystyle X_{1}\;\sim \;\mathrm {Pois} (\lambda _{1})}$ và ${\displaystyle X_{2}\;\sim \;\mathrm {Pois} (\lambda _{2})}$, thì hiệu ${\displaystyle Y=X_{1}-X_{2}}$ tuân theo phân phối Skellam.
• Nếu ${\displaystyle X_{1}\;\sim \;\mathrm {Pois} (\lambda _{1})\,}$ và ${\displaystyle X_{2}\sim \mathrm {Pois} (\lambda _{2})\,}$ là độc lập, và ${\displaystyle Y=X_{1}+X_{2}}$, thì phân phối của ${\displaystyle X_{1}}$ phụ thuộc điều kiện vào ${\displaystyle Y=y}$ là một phân phối nhị thức. Đặc biệt, ${\displaystyle X_{1}|(Y=y)\sim \mathrm {Binom} (y,\lambda _{1}/(\lambda _{1}+\lambda _{2}))\,}$. Tổng quát hơn, nếu X₁, X₂,..., X_n là các biến ngẫu nhiên Poisson với các tham số tương ứng là λ₁, λ₂,..., λ_n thì ${\displaystyle X_{i}\left|\sum _{j=1}^{n}X_{j}\right.\sim \mathrm {Binom} \left(\sum _{j=1}^{n}X_{j},{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right)}$
• Phân phối Poisson có thể được xem là một trường hợp hạn chế của phân phối nhị thức khi mà số lần thử (trials) tiến đến vô hạn và giá trị kì vọng của số lần thành công là giữ nguyên. Vì thế, nó có thể dùng để xấp xỉ cho phân phối nhị thức nếu n là đủ lớn và p là đủ nhỏ. Có một quy luật theo kinh nghiệm là phân phối Poisson có thể ước lượng tốt cho một phân phối nhị thức nếu n lớn hơn 20 và p là nhỏ hơn hoặc bằng 0.05. Cũng theo quy luật này, xấp xỉ được xem là rất chính xác nếu n ≥ 100 và np ≤ 10.^[1]
• Với giá trị đủ bé của λ, (ví dụ λ>1000), thì phân phối chuẩn với trung bình λ, và độ lệch λ, là một xấp xỉ rất chính xác cho phân phối Poisson. Nếu λ lớn hơn 10, thì phân phối chuẩn là một xấp xỉ tốt nếu ta thực hiện chèn thêm 1/2 vào, nghĩa là, P(X ≤ x), với x (viết thường) là một số nguyên không âm, sẽ được thay bởi P(X ≤ x + 0.5).

${\displaystyle F_{\mathrm {Poisson} }(x;\lambda )\approx F_{\mathrm {normal} }(x;\mu =\lambda ,\sigma ^{2}=\lambda )\,}$

Sự ra đời

Phân phối Poisson ra đời gắn liền với quá trình Poisson. Nó được áp dụng cho nhiều hiện tượng (có tính rời rạc) (nghĩa là số lần xuất hiện trong một khoảng (thời gian, không gian) cho trước đó phải là số nguyên 0, 1, 2, 3,...) với xác suất để sự kiện (hiện tượng) đó xảy ra là không đổi trong suốt khoảng (thời gian, không gian) đó. Các ví dụ sau được mô hình theo phân phối Poisson:

• Số lượng xe hơi đi ngang qua 1 điểm trên con đường trong một khoảng thời gian cho trước.
• Số lần gõ bị sai của khi đánh máy một trang giấy.
• Số cuộc điện thoại tại một trạm điện thoại trong mỗi phút.
• Số lần truy cập vào một máy chủ web trong mỗi phút.
• Số lần động vật bị chết do xe cộ cán phải trên mỗi đơn vị độ dài của một con đường.
• Số lần đột biến xảy ra trên một đoạn DNA sau khi chịu một lượng bức xạ..
• Số lượng cây thông trên mỗi đơn vị diện tích rừng hỗn hợp.
• Số lượng ngôi sao trong một thể tích không gian vũ trụ.
• Số lượng người lính bị chết do ngựa đá mỗi năm trông mỗi đội của kị binh Phổ. Ví dụ này rất nổi tiếng trong cuốn sách của Ladislaus Josephovich Bortkiewicz (1868–1931).
• Phân phối của các tế bào cảm quang trong võng mạc của mắt.
• Số lượng bóng đèn bị cháy trong một khoảng thời gian xác định.
• Số lượng virut có thể lây nhiễm lên một tế bào trong cấu trúc tế bào.
• Số lưộng phát minh của một nhà sáng chế trong suốt cuộc đời của họ.

Tại sao lại tồn tại phân phối này? — Luật của các sự kiện hiếm

Các tính chất

• Giá trị kì vọng của một biến ngẫu nhiên phân phối Poisson là λ và nó cũng chính là độ lệch. Các giá trị mômen cao hơn của phân phối Poisson chính là các đa thức Touchard trong λ, với các hệ số có ý nghĩa tổ hợp. Cụ thể là nếu khi giá trị kì vọng của phân phối Poisson là 1, thì công thức Dobinski nói rằng moment thứ n bằng với số phân hoạch của một tập hợp có kích thước là n.
• mode của một biến ngẫu nhiên phân phối Poisson với λ không là số nguyên thì bằng với ${\displaystyle \scriptstyle \lfloor \lambda \rfloor }$, chính là số nguyên lớn nhất không vượt quá λ. Nếu λ là số nguyên dương, thì modes chính là λ và λ − 1.
• Tổng của các biến ngẫu nhiên theo phân phối Poisson:

Nếu ${\displaystyle X_{i}\sim \mathrm {Poi} (\lambda _{i})\,}$ tuân theo phân phối Poisson với tham số ${\displaystyle \lambda _{i}\,}$ và ${\displaystyle X_{i}}$ là độc lập nhau, thì ${\displaystyle Y=\sum _{i=1}^{N}X_{i}\sim \mathrm {Poi} \left(\sum _{i=1}^{N}\lambda _{i}\right)\,}$ cũng tuân theo phân phối Poisson với tham số là tổng của các tham số thành phần.

• Hàm khởi tạo mômen của phân phối Poisson với giá trị kì vọng λ là

${\displaystyle \mathrm {E} \left(e^{tX}\right)=\sum _{k=0}^{\infty }e^{tk}f(k;\lambda )=\sum _{k=0}^{\infty }e^{tk}{\lambda ^{k}e^{-\lambda } \over k!}=e^{\lambda (e^{t}-1)}.}$

• Mọi nửa bất biến (cumulant) của phân phối Poisson bằng với giá trị kì vọng λ. Mômen giai thừa thứ n của phân phối Poisson là λⁿ.
• Phân phối Poisson chính là phân phối xác suất có thể chia hết vô hạn.
• Định hướng phân kì Kullback-Leibler giữa Poi(λ₀) và Poi(λ) được cho bởi

${\displaystyle \Delta (\lambda ||\lambda _{0})=\lambda \left(1-{\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda _{0}}{\lambda }}\log {\frac {\lambda _{0}}{\lambda }}\right).}$

Khởi tạo các biến ngẫu nhiên có phân phối Poisson

Một cách đơn giản để khởi tạo các số ngẫu nhiên theo phân phối Poisson được đưa ra bởi Knuth, xem tham khảo ở dưới.

algorithm poisson random number (Knuth):
 init:
Let L ← e−λ, k ← 0 and p ← 1.
 do:
k ← k + 1.
Generate uniform random number u and let p ← p × u.
 while p ≥ L.
 return k − 1.

Dù đơn giản, nhưng độ phức tạp của giải thuật là tuyến tính với λ. Nên có nhiều giải thuật khác giải quyết vấn đề này. Xem tham khảo tại sách của Ahrens & Dieter.

Ước lượng tham số

Hợp lý cực đại

Cho một mẫu gồm n giá trị được đo k_i chúng ta muốn ước lượng giá trị của tham số λ của tập hợp phân phối Poisson mà từ đó mẫu này được rút ra. Để tính giá trị hợp lý cực đại (maximum likelihood), ta tạo ra hàm log-likelihood

${\displaystyle L(\lambda )=\ln \prod _{i=1}^{n}f(k_{i}\mid \lambda )\!}$

${\displaystyle =\sum _{i=1}^{n}\ln \!\left({\frac {e^{-\lambda }\lambda ^{k_{i}}}{k_{i}!}}\right)\!}$

${\displaystyle =-n\lambda +\left(\sum _{i=1}^{n}k_{i}\right)\ln(\lambda )-\sum _{i=1}^{n}\ln(k_{i}!).\!}$

Lấy đạo hàm của L theo λ và cho nó bằng 0:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} \lambda }}L(\lambda )=0\iff -n+\left(\sum _{i=1}^{n}k_{i}\right){\frac {1}{\lambda }}=0\!}$

Giải tìm λ sẽ cho ta ước lượng hợp lý cực đại của λ:

${\displaystyle {\widehat {\lambda }}_{\mathrm {MLE} }={\frac {1}{n}}\sum _{i=1}^{n}k_{i}.\!}$

Vì mỗi quan sát có kì vọng λ theo ý nghĩa của mẫu. Vì thế nó là một ước lượng không lệch của λ.

Suy luận Bayes

Trong suy luận Bayes, tiên nghiệm liên hợp (conjugate prior) cho tham số λ của phân phối Poisson là phân phối Gamma. Nếu

${\displaystyle \lambda \sim \mathrm {Gamma} (\alpha ,\beta )\!}$

đại diện cho λ được phân phối theo mật độ Gamma g' được tham số hóa theo một tham số hình dạng (shape parameter) α và một tham số tỉ lệ (scale parameter) nghịch đảo β:

${\displaystyle g(\lambda \mid \alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\;\lambda ^{\alpha -1}\;e^{-\beta \,\lambda }\qquad {\mbox{for}}\ \lambda >0\,\!.}$

Thì, nếu cho cùng một mẫu gồm n giá trị được đo k_i như ở trên, và một tiên nghiệm của Gamma(α, β), thì phân phối hậu nghiệm (posterior distribution) là

${\displaystyle \lambda \sim \mathrm {Gamma} (\alpha +\sum _{i=1}^{n}k_{i},{\frac {1}{{\frac {1}{\beta }}+n}}).\!}$

"Luật số nhỏ"

Phân phối Poisson còn được gọi là luật số nhỏ vì nó là xác suất phân phối của số lần xuất hiện của một sự kiện mà rất hiếm khi xảy ra, nhưng cơ hội để xảy ra thì lại rất nhiều. Và The Law of Small Numbers là tiêu đề của cuốn sách viết bởi Ladislaus Bortkiewicz về phân phối Poisson, được xuất bản năm 1898. Vì thế, một số cho rằng phân phối Poisson nên được gọi là phân phối Bortkiewicz.^[2]

Tính toán gần đúng cho xác suất Poisson

Khi k lớn (>20) việc sử dụng xấp xỉ hàm logarit và lũy thừa là cần thiết. Ví dụ sau viết bằng Java.

/**Calculates an approximation of the Poisson probability.
 * @param mean - lambda, the average number of occurrences
 * @param observed - the actual number of occurences observed
 * @return ln(Poisson probability) - the natural log of the Poisson probability.
 */
public static double poissonProbabilityApproximation (double mean, int observed) {
	double k = observed;
	double a = k * Math.log(mean);
	double b = -mean;
	return a + b - factorialApproximation(k);
}

/**Srinivasa Ramanujan ln(n!) factorial estimation.
 * Good for larger values of n.
 * @return ln(n!)
 */
public static double factorialApproximation(double n) {
	if (n < 2.) return 0;
	double a = n * Math.log(n) - n;
	double b = Math.log(n * (1. + 4. * n * (1. + 2. * n))) / 6.;
	return a + b + Math.log(Math.PI) / 2.;
}

Nhiễu Poisson

Xem thêm

• Phân phối Poisson phức hợp
• Quá trình Poisson
• Hồi qui Poisson
• Lý thuyết hàng đợi
• Erlang distribution
• Phân phối Skellam.
• Incomplete gamma function dùng để tính CDF.
• Dobinski's formula
• Schwarz formula
• Bổ đề Robbins

Công cụ trực tuyến để minh họa hình ảnh cho phân phối Poisson

Phân phối Poisson có tương tác tại đại học Texas A&M (TAMU) Lưu trữ 2008-02-03 tại Wayback Machine

Chú thích

Tham khảo

• Donald E. Knuth (1969). Seminumerical Algorithms. The Art of Computer Programming, Volume 2. Addison Wesley.

• Joachim H. Ahrens, Ulrich Dieter (1974). “Computer Methods for Sampling from Gamma, Beta, Poisson and Binomial Distributions”. Computing. 12 (3): 223--246. doi:10.1007/BF02293108.

• Joachim H. Ahrens, Ulrich Dieter (1982). “Computer Generation of Poisson Deviates”. ACM Transactions on Mathematical Software. 8 (2): 163--179. doi:10.1145/355993.355997.

Liên kết ngoài

• “Law of rare events”. PlanetMath.

• Queueing Theory Basics
• M/M/1 Queueing System
• Engineering Statistics Handbook: Poisson Distribution
• xkcd webcomic involving a Poisson distribution
• Poisson Distribution at QWiki Lưu trữ 2007-11-01 tại Wayback Machine
• Poisson Derivation 1: Continuous limit of a Binomial distribution Lưu trữ 2007-11-01 tại Wayback Machine
• Poisson Derivation 2: Generating function approach Lưu trữ 2007-10-27 tại Wayback Machine
• Poisson Derivation 3: Summation of the waiting-time distribution Lưu trữ 2007-10-13 tại Wayback Machine
• Máy tính trực tuyến Phân phối Poisson

Bản mẫu:Statistics