Arkimedisk spiral

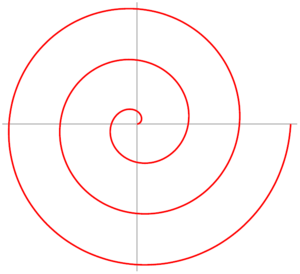
En arkimedisk spiral er i matematikk en plan kurve, en spiral hvor økningen i radien er like stor for hver omdreining.^[1] Kurven blir generert av et punkt som beveger seg med konstant hastighet på en stråle, samtidig som strålen roterer med konstant hastighet. Spiralen er oppkalt etter den greske matematikeren Arkimedes.

Kurveligning

I polarkoordinater ${\displaystyle (r,\theta )}$ er ligningen for Arkimedes' spiral

${\displaystyle r=a+b\theta \qquad \theta \in \lbrack \theta _{1},\theta _{2}\rbrack }$

der ${\displaystyle a}$ og ${\displaystyle b}$ er vilkårlige positive kurveparametre. En endring i ${\displaystyle a}$ vrir spiralen, ved å flytte startpunktet for spiralen. En endring i ${\displaystyle b}$ gir en endring i avstanden mellom suksessive omdreininger i spiralen.

I kartesiske koordinater kan en beskrive spiralen på forma

${\displaystyle {\begin{alignedat}{2}x(\theta )=(a+b\theta )\cos \theta \\y(\theta )=(a+b\theta )\sin \theta \end{alignedat}}}$

En arkimedisk spiral er eksempel på en transendental kurve, en kurve som ikke kan uttrykkes kun ved hjelp av polynomer.

Buelengde og krumning

Buelengden til kurven er definert ved

${\displaystyle s(\theta )=\int _{\theta _{1}}^{\theta }{\sqrt {x'^{2}+y'^{2}}}d\theta }$

der ${\displaystyle x'}$ og ${\displaystyle y'}$ er de deriverte av koordinatfunksjonene med hensyn på ${\displaystyle \theta }$. Fra definisjonen av spiralen følger

${\displaystyle s(\theta )=\int _{\theta _{1}}^{\theta }{\sqrt {a^{2}+b^{2}+2ab\theta +b^{2}\theta ^{2}}}d\theta }$

For en spiral som starter i origo er ${\displaystyle a=0}$ og ${\displaystyle \theta _{1}=0}$, og buelengden er dermed gitt ved:^[2]

${\displaystyle s(\theta )=b\int _{0}^{\theta }{\sqrt {1+\theta ^{2}}}d\theta ={\frac {b}{2}}\lbrack \theta {\sqrt {1+\theta ^{2}}}+\ln(\theta +{\sqrt {1+\theta ^{2}}})\rbrack }$

Krumningen er gitt ved^[2]

${\displaystyle \kappa (\theta )={\frac {2+\theta ^{2}}{b(1+\theta ^{2})^{\frac {3}{2}}}}}$

Historie

Den greske matematikeren Arkimedes (født ca. 287 f.Kr.) beskrev kurven i læreverket Om spiraler.^[3] Verket ble mye beundret, men også betraktet som det vanskeligste blant det Arkimedes skrev. Motivasjonen for studiet av spiralen var å bruke den til å utføre tredeling av en vinkel og kvadrering av en sirkel. Arkimedes ga æren for først å ha beskrevet kurven til vennen Konon, en matematiker i Aleksandria.^[3]

Referanser