 | 「長円」はこの項目へ転送されています。仏師については「長円 (仏師)」をご覧ください。 |
 円錐切断面の4つのタイプ(放物線(左)、楕円(中央)、円(中央)、双曲線(右))
円錐切断面の4つのタイプ(放物線(左)、楕円(中央)、円(中央)、双曲線(右)) 楕円(だえん、正字: 橢圓、英: ellipse)とは、平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線である。
基準となる2定点を焦点という。円錐曲線の一種である。
概要
2つの焦点が近いほど楕円は円に近づき、2つの焦点が一致したとき楕円はその点を中心とした円になる。そのため円は楕円の特殊な場合であると考えることもできる。
楕円の内部に2焦点を通る直線を引くとき、これを長軸という。長軸の長さを長径という。長軸と楕円との交点では2焦点からの距離の差が最大となる。また、長軸の垂直二等分線を楕円の内部に引くとき、この線分を短軸という。短軸の長さを短径という。
用語
- 長軸と短軸の交点は楕円の中心と呼ばれる。
- 長軸を中心で分けた2つの線分は半長軸と呼ばれ、その長さを長半径という。
- 短軸を中心で分けた2つの線分は半短軸と呼ばれ、その長さを短半径という。
- 短径と長径の比は楕円率と呼ばれる。
 楕円の長軸(緑線)と短軸(ピンク線)
楕円の長軸(緑線)と短軸(ピンク線) 楕円の方程式
2次元直交座標系で、原点 O が長軸と短軸の交点となる楕円は代数的に次のように書ける。これを標準形という。

a > b > 0 のとき、2a は長軸の長さ(長径)、2b は短軸の長さ(短径)となる。xy 平面上にグラフを書くと横長の楕円となる。また、焦点はx 軸上にあり、その座標は  となる。
となる。
b > a > 0 のときは逆に、2b が長軸の長さ(長径)、2a が短軸の長さ(短径)となる。したがって、xy 平面上にグラフを書くと縦長の楕円となる。また、焦点は y 軸上にあり、その座標は  となる。(a = bの時は円となる)
となる。(a = bの時は円となる)
頂点の座標は a ≠ b のとき  となる。
となる。
同じ楕円は、t を媒介変数とする媒介変数表示では、次のように表現できる。



ただし、t は (x,y) ベクトルのx軸に対する角度ではない(天体力学では離心近点角と呼ばれる)。
「緯度#更成緯度 (reduced latitude)」も参照
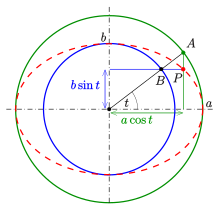 媒介変数表示により表された楕円上の点Pと媒介変数tの関係。tは点Pとx軸の角度とは異なる。
媒介変数表示により表された楕円上の点Pと媒介変数tの関係。tは点Pとx軸の角度とは異なる。 また、 と置くと、
と置くと、

となるので、下記の表現でも楕円を表すことができる。この場合uの範囲は[0,1]である。

複素平面Cにおいては,Cの二点 からの点
からの点 への 距離
への 距離 の和が
の和が であるものの軌跡である。
であるものの軌跡である。

楕円の幾何学的諸量
楕円の形状は離心率 e で表現される。

別途、扁平率 f でも表現できる。

楕円の面積 S は次のように表現できる。

楕円の周長 C は a > b のとき、第二種完全楕円積分を用いて次のように表現できる。

また  とおき、二項係数を使って、次のようにも表現できる(Gauss-Kummer級数)[1]。
とおき、二項係数を使って、次のようにも表現できる(Gauss-Kummer級数)[1]。

計算機で計算する場合に有用な式としては、分母が  の率で消える式が次のように導出されている[2]。
の率で消える式が次のように導出されている[2]。





近似式としては、シュリニヴァーサ・ラマヌジャンによる次の二式がある。簡便なものとしては、
![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}~\right]=\pi \left[3(a+b)-{\sqrt {10ab+3\left(a^{2}+b^{2}\right)}}~\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edd5aab14781b8a17ee124d24ad2c84c83da62d3)
があり、さらに良い近似として、次式がある。
![{\displaystyle C\approx \pi (a+b)\left[1+{\frac {3\left({\dfrac {a-b}{a+b}}\right)^{2}}{10+{\sqrt {4-3\left({\dfrac {a-b}{a+b}}\right)^{2}}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b74a5f2e1b75577d7b479e91e3666d61ee3ccf5c)
より一般的には、対応する角度の関数としての、周長の一部である楕円弧長は、第二種不完全楕円積分で表される。
楕円弧長と第二種不完全楕円積分の関係の詳細
楕円を媒介変数表示

で表した時、 から
から までの弧長
までの弧長 は
は

で求められる。これは、 の大小関係に関係なく成立する。
の大小関係に関係なく成立する。
この式は第二種不完全楕円積分で表す事ができるが、  の大小関係や
の大小関係や の範囲により場合分けが必要になる為、以下に詳述する。
の範囲により場合分けが必要になる為、以下に詳述する。
その前に、媒介変数表示について、補足しておく。 楕円の媒介変数表示には、通常

が用いられる。この場合、t = 0 では、点 をとり、 t =
をとり、 t =  では点
では点 をとるので、tはx軸の正の部分を基準線とする反時計方向の角度になっている。
をとるので、tはx軸の正の部分を基準線とする反時計方向の角度になっている。
一方、媒介変数表示は

とする事もでき、この場合、t = 0 では、点 をとり、 t =
をとり、 t =  では点
では点 をとるので、tはy軸の正の部分を基準線とする時計方向の角度になっている。
をとるので、tはy軸の正の部分を基準線とする時計方向の角度になっている。
第二種不完全楕円積分を


と表記する。 さらに、楕円上の点を指定する指標として、 ベクトルのx軸に対する角度
ベクトルのx軸に対する角度 も導入する。
も導入する。
- (
 )
)
A)  の時
の時

楕円(の右半分)を

で表す。 は点
は点 から
から が与える点までの弧長となっている。
が与える点までの弧長となっている。
この時



となる。 が点
が点 を最大の終点とする積分になる事を考慮し、 場合分けをし積分範囲を決めると、次のようになる。
を最大の終点とする積分になる事を考慮し、 場合分けをし積分範囲を決めると、次のようになる。
- i)



- ii)



- iii)



ここで

- (ただし、
 とする)
とする)
である。
B)  の時
の時

楕円(の右半分)を

で表す。 は点
は点 から
から が与える点までの弧長となっている。
が与える点までの弧長となっている。
この時



となる。 が点
が点 を始点とする積分になる事を考慮し、 場合分けをし積分範囲を決めると、次のようになる。
を始点とする積分になる事を考慮し、 場合分けをし積分範囲を決めると、次のようになる。
- i)



- ii)



- iii)



ここで

- (ただし、
 とする)
とする)
である。
作図法
 糸を使った作図例
糸を使った作図例 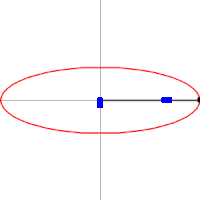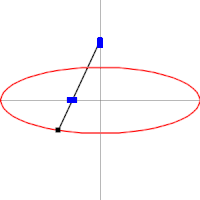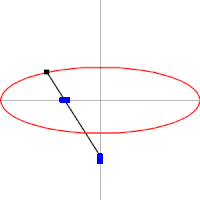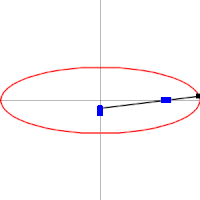 アルキメデスの楕円コンパスen:Trammel of Archimedesを使った作図例
アルキメデスの楕円コンパスen:Trammel of Archimedesを使った作図例 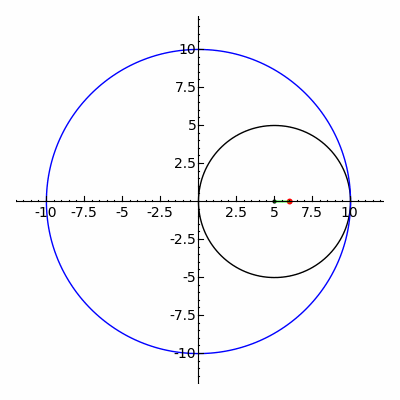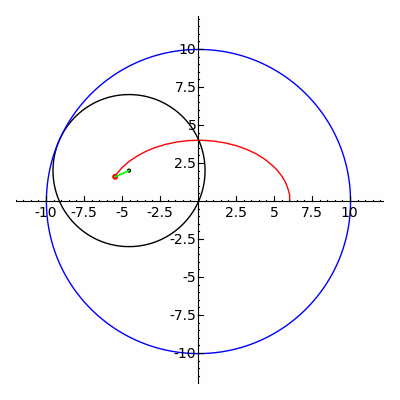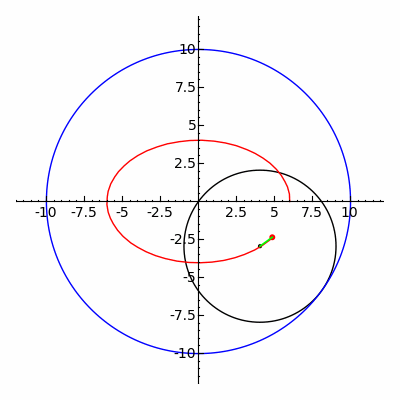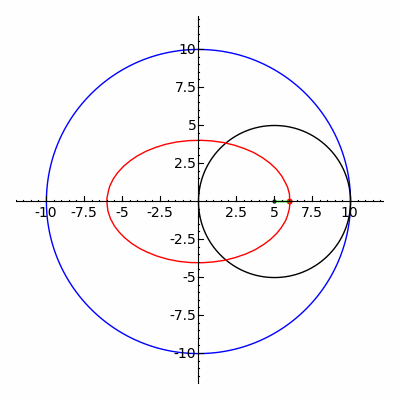 楕円は内トロコイドの特殊な場合として表される。図は rc = 10, rm = 5, rd = 1 の場合。
楕円は内トロコイドの特殊な場合として表される。図は rc = 10, rm = 5, rd = 1 の場合。 2つの焦点に、焦点間距離よりも長い1本の糸の両端をそれぞれ固定し、糸が張る状態で節に取り付けた筆記具を動かす。この他、楕円コンパス、楕円テンプレートなどを使って作図はできる。
また、内トロコイドの特殊な場合に楕円が描画される。
歴史
中国語で楕円の楕は「木の切り株」の意味で「木の切り口」の 形から名付けられたと考えられている。 日本では田畑の実際の形から「飯櫃」「平卵形」などと呼ばれていたが、関孝和は「側円」と呼んだ。江戸時代には側円と呼ばれ明治になって楕円と呼ばれるようになった。
脚注
- ^ Weisstein, Eric W. "Gauss-Kummer Series". mathworld.wolfram.com (英語).
- ^ Cetin Hakimoglu-Brown iamned.com math page
参考文献
- 『曲線の事典 性質・歴史・作図法』礒田正美、Maria G. Bartolini Bussi編、田端毅、讃岐勝、礒田正美著:共立出版、2009年 ISBN 9784320019072
関連項目
外部リンク
ウィキメディア・コモンズには、楕円に関連するメディアおよびカテゴリがあります。
- 楕円歯車: オランダの数学者en:Frans van Schootenが著書 "De organica conicarum sectionum in plano descriptione tractatus" において紹介している機構
典拠管理データベース: 国立図書館  | - フランス
- BnF data
- ドイツ
- イスラエル
- アメリカ
|
|---|



































![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}~\right]=\pi \left[3(a+b)-{\sqrt {10ab+3\left(a^{2}+b^{2}\right)}}~\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edd5aab14781b8a17ee124d24ad2c84c83da62d3)
![{\displaystyle C\approx \pi (a+b)\left[1+{\frac {3\left({\dfrac {a-b}{a+b}}\right)^{2}}{10+{\sqrt {4-3\left({\dfrac {a-b}{a+b}}\right)^{2}}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b74a5f2e1b75577d7b479e91e3666d61ee3ccf5c)

























































