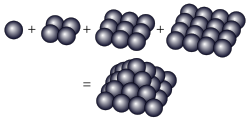
 1 + 4 + 9 + 16 = 30 は四角錐数
1 + 4 + 9 + 16 = 30 は四角錐数 四角錐数(しかくすいすう、square pyramidal number)は球を右図のように1段目に1個、2段目に4個、3段目に9個、…というように正四角錐の形に積んだとき、そこに含まれる球の総数にあたる自然数である。つまり1から順に平方数をいくつか加えた数のことである。
四角錐数を小さい順に列記すると
- 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, …(オンライン整数列大辞典の数列 A330)
例: 1, 5 (=1+4), 14 (=1+4+9), 30 (=1+4+9+16), 55 (=1+4+9+16+25)
性質
n番目の四角錐数は 1 から n 番目の平方数 n2 までの和に等しいので

で表される。これは以下のように証明される。まず n 番目の三角数を Tn 、n 番目の四角錐数を Sn とすると、

となるので、

が得られる。
また組み合わせの記号を用いると  となる。これは四角錐数が連続する三角錐数の和で表せることを示しており、四角数が連続する三角数の和で表せることと類似の定理である。
となる。これは四角錐数が連続する三角錐数の和で表せることを示しており、四角数が連続する三角数の和で表せることと類似の定理である。
四角錐数は1から順に奇数-奇数-偶数-偶数 といった順番の繰り返しで現れる。
四角錐数のうち三角数でもある数は 1, 55, 91, 208335 の4つのみである。(オンライン整数列大辞典の数列 A039596)
四角錐数のうち平方数でもある数は 1 と 4900 (24番目の四角錐数)の 2 つのみである。また四角錐数でなおかつ三角錐数でもある数は 1 のみである。
n × n マスの方眼の中に含まれる正方形の数は n 番目の四角錐数に等しい。



- …
と無限に続く足し算の等式はタルタリアの三角形と呼ばれる。上から n 段目の等式の値は n 番目の四角錐数の3倍である。



- …
と無限に続く自乗和の等式も同じ名で呼ばれる。等式の値は n 番目の四角錐数の 12n(n + 1) + 1 倍である。この値は1から n までの立方和の 16(n + 1/2) 倍と n 番目の四角錐数の和にも等しく、1から n までの4乗和(n 番目の四角錐数の {3n(n + 1) - 1}/5 倍)の20倍と n 番目の四角錐数の5倍の和にも等しい。1段目から n 段目までの総和は、足し算の三角形のそれの1/3(即ち1番目から n 番目までの四角錐数の総和)の 8n(n + 2) + 1 倍である。
関連項目
外部リンク
- Weisstein, Eric W. "Square Pyramidal Number". mathworld.wolfram.com (英語).


















