Diagramma di Bode

Un diagramma di Bode è una rappresentazione grafica della risposta in frequenza di un sistema lineare tempo-invariante (LTI) e che consiste in due grafici che rappresentano rispettivamente l'ampiezza (o modulo) e la fase della funzione complessa di risposta in frequenza. Ricordiamo che si parla di risposta in frequenza quando la funzione di trasferimento di un sistema lineare tempo invariante viene sollecitata da un ingresso di tipo sinusoidale con pulsazione ${\displaystyle \omega }$ al variare di questa.

Il nome di questo tipo di rappresentazione è dovuto allo scienziato statunitense Hendrik Wade Bode, pioniere nello studio della teoria dei controlli e delle telecomunicazioni elettroniche.

Contrariamente alla rappresentazione polare, o diagramma di Nyquist, la rappresentazione di modulo e fase della funzione di trasferimento non avviene su un solo piano complesso, ma in due distinti che hanno entrambi in ascissa, come variabile indipendente, la frequenza o la pulsazione e in ordinata il modulo dell'ampiezza usualmente espressa in decibel o la fase espressa in gradi o radianti.

I due diagrammi possono raramente essere modificati l'uno dall'altro indipendentemente: se si modifica la risposta in modulo molto probabilmente verrà modificata la risposta in fase e viceversa. Per sistemi a fase minima è possibile risalire al diagramma della risposta della fase dal diagramma della risposta del modulo tramite la trasformata di Hilbert.

Il diagramma di Bode trova applicazione, ad esempio, nella teoria dei controlli, nella teoria dei sistemi, nella progettazione di filtri e amplificatori.

Per facilitare lo studio su un elevato spettro di pulsazioni sia il diagramma del modulo sia il diagramma della fase vengono rappresentati su carta logaritmica o semilogaritmica divisa in decadi. La carta semilogaritmica è caratterizzata dal fatto che la distanza che separa due valori ${\displaystyle \omega _{a}}$ e ${\displaystyle \omega _{b}}$ è proporzionale alla differenza tra i logaritmi (solitamente in base 10) di ${\displaystyle \omega _{a}}$ e ${\displaystyle \omega _{b}}$. Fatte queste premesse, una possibile rappresentazione dei valori della pulsazione sulla carta semilogaritmica potrebbe essere

I vantaggi nell'uso di diagrammi logaritmici sono sostanzialmente la possibilità di rappresentare col dovuto dettaglio grandezze che variano in campi notevolmente estesi e la possibilità di semplificare i calcoli di moltiplicazione che nel caso di logaritmi si riconducono semplicemente a somme.

Nel diagramma del modulo si rappresenta, sulla carta semilogaritmica, la pulsazione sull'asse delle ascisse, mentre su quello delle ordinate il modulo espresso in decibel, cioè il modulo espresso secondo la formula^[1]

${\displaystyle \left|{F(j\omega )}\right|_{dB}=20\log _{10}\left({\left|{F(j\omega )}\right|}\right)}$

Nel diagramma della fase si rappresentano le ampiezze assunte dall'argomento di F per diversi valori di ${\displaystyle \omega }$. Anche in questo caso è utile servirsi della carta semilogaritmica indicando sull'asse delle ascisse le pulsazioni e sull'asse delle ordinate le ampiezze, solitamente espresse in gradi.

Per tracciare il diagramma reale di Bode, sia del modulo, sia della fase, è richiesta una quantità particolarmente elevata di calcoli, dovendo valutare il modulo e la fase della funzione F per un ventaglio di valori della pulsazione molto ampio, e questo, in assenza di un calcolatore elettronico che esegue parecchi calcoli in breve tempo, può risultare molto difficile o comunque dispendioso in termini di tempo. Per ovviare a questo problema è prassi comune quella di disegnare i diagrammi di Bode a partire dai diagrammi asintotici e approssimando il comportamento dei grafici reali da questi ultimi.

La funzione di trasferimento di un sistema è una funzione frazionaria sicuramente propria, nella quale compaiono a numeratore le uscite e a denominatore gli ingressi. Per studiare con maggiore facilità una funzione di trasferimento è utile riportarla in forma canonica o forma di Bode. Questa particolare forma è costituita da una serie fattorizzata di monomi, binomi e trinomi espressi nella variabile complessa di Laplace. Essa assume la forma:

${\displaystyle G(s)={\frac {\mu }{s^{g}}}\cdot {\frac {\prod \limits _{i=1}^{p}{\left({1+T_{i}s}\right)}\cdot \prod \limits _{i=1}^{q}{\left({{\frac {s^{2}}{\omega _{n_{i}}^{2}}}+2\xi _{i}{\frac {s}{\omega _{n_{i}}}}+1}\right)}}{\prod \limits _{i=1}^{m}{\left({1+\tau _{i}s}\right)}\cdot \prod \limits _{i=1}^{w}{\left({{\frac {s^{2}}{\omega _{n_{i}}^{2}}}+2\zeta _{i}{\frac {s}{\omega _{n_{i}}}}+1}\right)}}}}$

Il significato dei vari membri di questa funzione sono:

• ${\displaystyle \mu }$: Valore costante che esprime il guadagno della funzione di trasferimento
• ${\displaystyle s^{g}}$: Zeri o poli nell'origine, a seconda del valore assunto da g.
• ${\displaystyle {\left({1+T_{i}s}\right)}}$: Zero reale della funzione di trasferimento.
• ${\displaystyle {\left({1+\tau _{i}s}\right)}}$: Polo reale della funzione di trasferimento.
• ${\displaystyle {\left({{\frac {s^{2}}{\omega _{n}^{2}}}+2\xi {\frac {s}{\omega _{n}}}+1}\right)}}$: Coppia di zeri complessi coniugati.
• ${\displaystyle {\left({{\frac {s^{2}}{\omega _{n}^{2}}}+2\zeta {\frac {s}{\omega _{n}}}+1}\right)}}$: Coppia di poli complessi coniugati.

Effettuando la restrizione del dominio da ${\displaystyle s}$ a ${\displaystyle j\omega }$, sotto le condizioni del prolungamento analitico, si passa alla forma canonica, che permette di studiare più facilmente l'andamento della funzione trovandosi ora nel dominio della trasformata di Fourier. Su scala semilogaritmica (misurando l'ampiezza in dB), infatti, tutte le produttorie si trasformano in sommatorie ed è possibile studiare separatamente ciascun membro della funzione, che porta dei contributi differenti sia sul diagramma del modulo, sia sul diagramma della fase. Il modulo di H(s), infatti, sarà la somma algebrica dei moduli di tutti i fattori così come la fase sarà la somma algebrica delle fasi di tutti i fattori.

La funzione di trasferimento dopo aver effettuato la sostituzione appare nella forma:

${\displaystyle H(j\omega )=k\cdot {\frac {\prod _{i=1}^{p}(1+T_{i}j\omega )\prod _{i=1}^{q}({\frac {(j\omega )^{2}}{\omega _{n_{i}}^{2}}}+{\frac {2\xi _{i}}{\omega _{n_{i}}}}j\omega +1)}{(j\omega )^{g}\prod _{i=1}^{\mu }(1+\tau _{i}j\omega )\prod _{i=1}^{w}({\frac {(j\omega )^{2}}{\omega _{n_{i}}^{2}}}+{\frac {2\zeta _{i}}{\omega _{n_{i}}}}j\omega +1)}}}$

Viene data la funzione di trasferimento ${\displaystyle G(s)}$ e si vuole trovare il guadagno, il tipo, gli zeri o i poli nell'origine, gli zeri e i poli reali e gli zeri ed i poli complessi coniugati.

${\displaystyle G(s)={\frac {8s^{2}\left({1+s}\right)\left({{\frac {s^{2}}{100}}+2\cdot 0{,}3{\frac {s}{10}}+1}\right)}{\left({1+0{,}2s}\right)^{2}}}}$

Per prima cosa conviene riscrivere la funzione in un'espressione che "assomigli" di più a quella canonica scritta sopra quindi

${\displaystyle G(s)={\frac {8s^{2}\left({1+s}\right)\left({{\frac {s^{2}}{100}}+2\cdot 0{,}3{\frac {s}{10}}+1}\right)}{\left({1+0{,}2s}\right)^{2}}}={\frac {8}{s^{-2}}}\cdot {\frac {\left({1+s}\right)\left({{\frac {s^{2}}{100}}+2\cdot 0{,}3{\frac {s}{10}}+1}\right)}{\left({1+0{,}2s}\right)\left({1+0{,}2s}\right)}}}$

Da cui si riconosce subito che il guadagno è ${\displaystyle \mu =8}$ e il tipo è ${\displaystyle g=-2}$ (cioè ci sono due zeri nell'origine). Si vede poi lo zero reale ${\displaystyle s=-1}$ e il doppio polo reale ${\displaystyle s=-5}$. Infine vi è la presenza di una coppia di zeri complessi coniugati con pulsazione naturale ${\displaystyle \omega _{n}=10}$ e smorzamento ${\displaystyle \xi =0{,}3}$.

Il grafico del guadagno di una funzione di trasferimento appare, molto semplicemente, come una retta orizzontale di modulo ${\displaystyle 20\log _{10}\left|\mu \right|dB}$ e un'altra di ampiezza ${\displaystyle \arg \left(\mu \right)}$.

Si vuole tracciare il diagramma reale di Bode della funzione di trasferimento ${\displaystyle G(s)=2}$

Il diagramma del modulo è una retta orizzontale di ordinata uguale a ${\displaystyle 20\log _{10}\left|2\right|\simeq 6dB}$

Il diagramma della fase è anch'esso una retta orizzontale di ordinata uguale a ${\displaystyle \arg \left(2\right)=0^{\circ }}$

I poli di una funzione di trasferimento si definiscono come le radici del denominatore (e quindi dell'ingresso). Dal momento che stiamo studiando i poli generati da ${\displaystyle (j\omega )^{m}}$, siamo nel caso di poli situati in 0 e con molteplicità m. Per semplicità di studio, ci limitiamo ad analizzare il caso ${\displaystyle m=1}$, lasciando a dopo le considerazioni su una possibile molteplicità m > 1.

I poli in zero influiscono sull'andamento della funzione di trasferimento nel seguente modo:

${\displaystyle {\bigg |}{\frac {1}{(j\omega )^{m}}}{\bigg |}_{dB}=20m\log _{10}{{\bigg |}{\frac {1}{j\omega }}{\bigg |}}=-20m\log _{10}{|\omega |}}$

Si tratta pertanto di una retta con pendenza -20 dB/decade (o 6 dB/ottava) incidente l'asse delle ascisse in ${\displaystyle \omega =1}$

${\displaystyle \phi {\bigg (}{\frac {1}{j\omega }}{\bigg )}=\arg {\bigg (}{\frac {1}{j\omega }}{\bigg )}=-\arg(j\omega )=-{\frac {\pi }{2}}}$

Nel caso (più generale) in cui m > 1 si può "aggirare" il problema pensando che ${\displaystyle (j\omega )^{m}=j\omega \cdot j\omega \cdot \ldots \cdot j\omega }$. Pertanto, poiché il diagramma di Bode viene rappresentato su scala semilogaritmica, si può pensare di sommare m contributi di fattori monomi del tutto simili a quello preso ora in esame.

Questa tesi viene sostenuta dal fatto che, rieseguendo i conti di modulo e fase svolti poco sopra mantenendo ${\displaystyle m\neq 0}$, si ottiene:

${\displaystyle {\bigg |}{\frac {1}{(j\omega )^{m}}}{\bigg |}_{dB}=-m\cdot 20\log _{10}|\omega |}$

${\displaystyle \phi {\bigg (}{\frac {1}{(j\omega )^{m}}}{\bigg )}=-m{\frac {\pi }{2}}}$

Si vuole tracciare il diagramma della funzione di trasferimento ${\displaystyle G(s)={\frac {2}{s}}}$

Modulo

In tal caso essendo ${\displaystyle s=j\omega }$ e

${\displaystyle G(j\omega )={\frac {2}{j\omega }}}$

allora il modulo risulta:

${\displaystyle |G(j\omega )|=|{\frac {2}{j\omega }}|={\frac {2}{|j\omega |}}={\frac {2}{\omega }}}$

con ${\displaystyle \omega \in \mathbb {R} ^{+}}$. Pertanto:

${\displaystyle |G(j\omega )|_{dB}=20\log _{10}{\frac {2}{\omega }}}$

e per

${\displaystyle \omega \rightarrow 0^{+}\Rightarrow |G(j\omega )|_{dB}\rightarrow +\infty }$

mentre per

${\displaystyle \omega \rightarrow +\infty \Rightarrow |G(j\omega )|_{db}\rightarrow -\infty }$,

inoltre per ${\displaystyle \omega =2}$ radianti al secondo

${\displaystyle |G(j\omega )|_{db}=0}$.

Come si può osservare dal diagramma, la pendenza è -1 sempre.

Fase

Poiché ${\displaystyle G(j\omega )=-j{\frac {2}{\omega }}}$ è immaginario puro e ${\displaystyle \omega \in \mathbb {R} ^{+}}$ è sempre positivo, allora i numeri complessi, al variare di ${\displaystyle \omega }$, sono sulla semiretta immaginaria negativa e quindi la loro fase è -90 sempre.

Gli zeri dei binomi posti a numeratore influiscono sull'andamento della funzione di trasferimento in modo non lineare. Può essere però comodo, per semplificare i conti, studiare un andamento approssimato del modulo e della fase, tenendo conto in seguito dell'errore massimo che si può commettere con questa semplificazione.

Modulo

${\displaystyle {\begin{aligned}|1+j\omega \tau |_{dB}&=20\log _{10}{|1+j\omega \tau |}\\&=20\log _{10}{\sqrt {1+\omega ^{2}\tau ^{2}}}\\&=10\log _{10}{\left(1+\omega ^{2}\tau ^{2}\right)}\\&=10\log _{10}{\left(1+{\frac {\omega ^{2}}{\omega _{B}^{2}}}\right)}\end{aligned}}}$

ponendo poi ${\displaystyle \omega _{B}=1/\tau }$

Si possono verificare ora due casi:

${\displaystyle |1+j\omega \tau |_{dB}={\begin{cases}\sim 10\log _{10}{1}=0&{\mbox{se }}\omega \ll \omega _{B}\\\sim 10\log _{10}{\omega ^{2}\tau ^{2}}=20\log _{10}{\omega \tau }&{\mbox{se }}\omega \gg \omega _{B}\end{cases}}}$

Ciò significa che il diagramma di Bode approssimato per un termine binomio posto a numeratore della funzione di trasferimento consiste di una spezzata che ha valore 0 per tutte le ${\displaystyle \omega <{1 \over |\tau |}}$ e che cresce linearmente di 20 dB/decade (o 6 dB/ottava) per tutte le ${\displaystyle \omega >{1/|\tau |}}$.

È naturale, ora, chiedersi quale sia l'errore massimo che si commette effettuando questa approssimazione. L'errore massimo è commesso proprio nel caso in cui ${\displaystyle \omega =\omega _{B}}$. Infatti, se ${\displaystyle \omega =\omega _{B}}$

${\displaystyle \implies |1+j\omega \tau |_{dB}=10\log _{10}{2}\cong 3dB}$

Siamo pertanto sicuri che, nell'approssimazione dell'andamento del modulo di un termine binomio con una spezzata, non si commette un errore maggiore di 3dB.

Fase

Un filtro passa basso RC, per esempio, ha la seguente risposta in frequenza:

${\displaystyle H(f)={\frac {1}{1+j2\pi fRC}}}$

La frequenza di taglio indicata dal punto f_c (in hertz) ha valore pari a

${\displaystyle f_{\mathrm {c} }={1 \over {2\pi RC}}}$.

L'approssimazione asintotica del diagramma di Bode consiste di due linee:

• per frequenze minori di f_c è una linea orizzontale a 0 dB,
• per frequenze maggiori di f_c è una linea con una pendenza di −20 dB per decade.

Queste due linee si incontrano alla frequenza di taglio. Dal diagramma si vede che per frequenze molto al disotto della frequenza di taglio il circuito ha un'attenuazione di 0dB, cioè il filtro non modifica il modulo del segnale. Frequenze al disopra della frequenza di taglio sono attenuate in misura maggiore tanto più si sale in frequenza.

Vediamo ora, in pratica, come si procede per tracciare un diagramma asintotico di Bode da cui poi si può tracciare, con buona approssimazione, quello reale. La spiegazione viene fatta seguendo un esempio pratico: si vuole tracciare il diagramma asintotico di Bode del modulo e della fase della funzione di trasferimento

${\displaystyle G(s)={\frac {10(1-0,05s)}{\left({1+s}\right)\left({1+0,5s}\right)}}={\frac {10}{s^{0}}}\cdot {\frac {\left({1-0,05s}\right)}{\left({1+s}\right)\left({1+0,5s}\right)}}}$

Per prima cosa mettiamo in evidenza tutte le informazioni che ci servono.

Si trova molto semplicemente calcolando ${\displaystyle \mu =G\left(0\right)}$ e poi trasformandolo in decibel con la formula ${\displaystyle \left|\mu \right|=20\log _{10}\mu }$ In questo caso ${\displaystyle \mu =10}$ da cui ${\displaystyle \left|\mu \right|=20\log _{10}10=20dB}$

Occorre guardare il tipo, ovvero l'esponente (solitamente si indica con la lettera g) relativo al polo nell'origine. In questo caso ${\displaystyle s^{0}}$ quindi il tipo è zero. La pendenza iniziale è uguale a ${\displaystyle -g=0}$.

Se il guadagno statico μ è minore di 0

${\displaystyle -180^{\circ }-g\cdot 90^{\circ }}$

Al contrario, se μ è maggiore o uguale a 0

${\displaystyle 0^{\circ }-g\cdot 90^{\circ }}$

Si individuano a questo punto gli zeri e i poli della funzione di trasferimento:

${\displaystyle {\rm {z}}_{\rm {1}}{\rm {=+20}}}$

${\displaystyle {\rm {p}}_{\rm {1}}{\rm {=-1}}}$

${\displaystyle {\rm {p}}_{\rm {2}}{\rm {=-2}}}$

I poli e gli zeri sono tutti reali (non complessi) e non nell'origine. Si inseriscono questi valori in una tabella dove sono divisi i poli dagli zeri e quelli a parte reale positiva da quelli a parte reale negativa da quelli nell'origine.

È data dal numero totale di zeri meno il numero totale di poli. Non è necessaria per tracciare il diagramma del modulo ma consente di verificare la correttezza dell'esercizio. In questo caso 1 – 2 = – 1.

Tracciamo ora i diagrammi asintotici di Bode sulla carta semilogaritmica.

Partiamo considerando una retta con pendenza iniziale 0 e che passa per il punto iniziale 20dB (significa che nel punto di pulsazione 1 ha modulo 20dB).

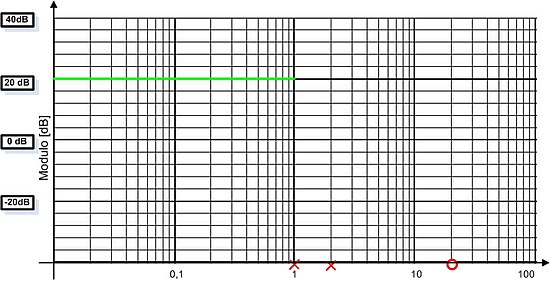
In corrispondenza di ω=1 troviamo un polo, quindi la pendenza del diagramma del modulo si abbassa di 20dB per decade. Lo stesso accade in ω=2, dove la pendenza scende di altri 20 dB per decade fino a ω=20, dove troviamo uno zero che aumenta la pendenza del diagramma di 20dB per decade.

Possiamo ora tracciare il diagramma della fase. Sapendo che il diagramma ha fase iniziale 0° traccio la prima parte del grafico asintotico.

In corrispondenza di ω=1 troviamo un polo a parte reale negativa che fa abbassare il diagramma di 90° così come accade in ω=2 e, successivamente, in ω=20 per via dello zero a parte reale positiva. I “+” e i “-“ riportati nelle caselle azzurre nella tabella servono proprio ad evidenziare quali singolarità (poli o zeri) fanno aumentare o diminuire di 90° il diagramma asintotico della fase.

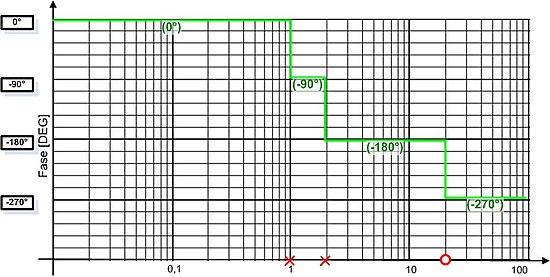
Con lo zero si abbassa di ulteriori 90° in quanto questo è instabile, avendo la parte reale positiva. Inoltre il comportamento della fase nei diagrammi di Bode per i poli con parte reale positiva e gli zeri con parte reale negativa è l'inverso di quello antecedentemente descritto.

• Diagramma di Nyquist
• Luogo delle radici

• Wikimedia Commons contiene immagini o altri file su Diagramma di Bode

• Bode Plot Applet - Mostra il grafico di modulo e fase dati i coefficienti della funzione di trasferimento