Racine d'un nombre

En mathématiques, une racine n-ième d'un nombre a est un nombre b tel que bⁿ = a, où n est un entier naturel non nul.

Selon que l'on travaille dans l'ensemble des réels positifs, l'ensemble des réels ou l'ensemble des complexes, le nombre de racines n-ièmes d'un nombre peut être 0, 1, 2 ou n.

Pour un nombre réel a positif, il existe un unique réel b positif tel que bⁿ = a. Ce réel est appelé la racine n-ième de a (ou racine n-ième principale de a) et se note ⁿ√a avec le symbole radical (√ ) ou a^1/n. La racine la plus connue est la racine carrée d'un réel. Cette définition se généralise pour a négatif et b négatif à condition que n soit impair.

Le terme de racine d'un nombre ne doit pas être confondu avec celui de racine d'un polynôme qui désigne la (ou les) valeur(s) où le polynôme s'annule.

Racine d'un réel

Racine carrée

Pour tout réel r strictement positif, l'équation x² = r admet deux solutions réelles opposées, et lorsque r = 0, l'équation x² = 0 admet comme seule solution 0.

La racine carrée d'un réel positif r est par définition l'unique solution réelle positive de l'équation x² = r d'inconnue x.

Elle est notée √r.

Exemples

• La racine carrée de deux est √2 = 1,414 213 56….
• Celle de trois est √3 = 1,732 050 80….

Racine cubique

La racine cubique d'un réel r quelconque est l'unique racine réelle de l'équation

${\displaystyle x^{3}-r=0}$ d'inconnue x.

Elle est notée ${\displaystyle {\sqrt[{3}]{r}}}$ .

Exemple :

• On a ${\displaystyle {\sqrt[{3}]{-8}}=-2}$. En effet ${\displaystyle -2}$ est le seul nombre réel dont la puissance troisième est égale à ${\displaystyle -8}$.

Racine n-ième d'un nombre réel positif

Pour tout entier naturel non nul ${\displaystyle n}$, l'application ${\displaystyle x\mapsto x^{n}}$ est une bijection de ${\displaystyle \mathbb {R} _{+}}$ sur ${\displaystyle \mathbb {R} _{+}}$ et donc pour tout réel ${\displaystyle r}$ positif, l'équation ${\displaystyle x^{n}=r}$ admet une unique solution dans ${\displaystyle \mathbb {R} _{+}}$.

La racine énième (ou racine n-ième) d'un réel r positif (r ≥ 0, n > 0) est l'unique solution réelle positive de l'équation

${\displaystyle x^{n}-r=0}$ d'inconnue x.

Elle est notée ${\displaystyle {\sqrt[{n}]{r}}}$.

Remarquons que la racine n-ième de ${\displaystyle r}$ est aussi l'unique racine positive du polynôme ${\displaystyle X^{n}-r}$.

Lorsque n est pair, l'équation

${\displaystyle x^{n}-r=0}$ d'inconnue x

possède deux solutions qui sont ${\displaystyle {\sqrt[{n}]{r}}}$ et ${\displaystyle -{\sqrt[{n}]{r}}}$.

Lorsque n est impair, l'équation

${\displaystyle x^{n}-r=0}$ d'inconnue x

ne possède qu'une seule solution ${\displaystyle {\sqrt[{n}]{r}}}$.

Racine n-ième d'un nombre réel négatif

Le traitement des racines de nombres négatifs n'est pas uniforme. Par exemple, il n'existe pas de racine carrée réelle de -1 puisque pour tout réel ${\displaystyle x}$, ${\displaystyle x^{2}+1>0}$, mais la racine cubique de -27 existe et est égale à -3.

Pour tout entier naturel impair ${\displaystyle n}$, l'application ${\displaystyle x\mapsto x^{n}}$ est une bijection de ${\displaystyle \mathbb {R} }$ sur ${\displaystyle \mathbb {R} }$ donc tout nombre réel admet exactement une racine ${\displaystyle n}$-ième.

Pour tout entier naturel impair ${\displaystyle n}$, la racine énième (ou racine ${\displaystyle n}$-ième) d'un réel ${\displaystyle r}$ quelconque est l'unique solution réelle de l'équation

${\displaystyle x^{n}-r=0}$

d'inconnue ${\displaystyle x}$.

Il s'ensuit que les racines d'ordres impairs de nombres réels négatifs sont négatives.

Remarquons que pour les entiers naturels impairs ${\displaystyle n}$ et pour tout réel ${\displaystyle a}$, on a

${\displaystyle {\sqrt[{n}]{-a}}=-{\sqrt[{n}]{a}}}$.

Le besoin de travailler avec des racines de nombres négatifs a conduit à la mise en place des nombres complexes, mais il y a également dans le domaine des nombres complexes des restrictions pour les racines. Voir ci-dessous.

Les propriétés des racines

Les règles de calcul des racines découlent des propriétés des puissances.

Pour les nombres strictement positifs, ${\displaystyle a}$ et ${\displaystyle b}$, on a les règles de calcul suivantes :

• ${\displaystyle {\sqrt[{n}]{a}}\cdot {\sqrt[{n}]{b}}={\sqrt[{n}]{a\cdot b}}}$
• ${\displaystyle {\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{m\cdot n}]{a}}}$
• ${\displaystyle {\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}={\sqrt[{n}]{\frac {a}{b}}}}$
• ${\displaystyle \left({\sqrt[{n}]{a}}\right)^{m}={\sqrt[{n}]{a^{m}}}}$

Dans le cas des nombres négatifs, ces règles de calcul ne pourront être appliquées que si ${\displaystyle m}$ et ${\displaystyle n}$ sont des nombres impairs. Dans le cas des nombres complexes, elles sont à éviter.

Exposant fractionnaire

Dans l'ensemble des réels strictement positifs, le nombre qui, élevé à la puissance n, donne a est noté ${\displaystyle {\sqrt[{n}]{a}}}$. L'idée est de noter ce nombre comme une puissance de a, quitte à prendre un exposant non entier. Il s'agissait donc de trouver un exposant p tel que ${\displaystyle \left(a^{p}\right)^{n}=a}$. En utilisant des opérations connues sur des exposants entiers que l'on généraliserait à des exposants non entiers, on obtiendrait ${\displaystyle a^{pn}=a^{1}}$, soit pn = 1 et ${\displaystyle p={\frac {1}{n}}}$.

Ainsi on peut noter la racine carrée de a , ${\displaystyle {\sqrt {a}}}$ ou ${\displaystyle a^{\frac {1}{2}}}$, la racine cubique de a , ${\displaystyle {\sqrt[{3}]{a}}}$ ou ${\displaystyle a^{\frac {1}{3}}}$ et la racine n-ième de a , ${\displaystyle {\sqrt[{n}]{a}}}$ ou ${\displaystyle a^{\frac {1}{n}}}$.

Cette extension des valeurs possibles pour l'exposant est due au travail de Newton et Leibniz^[1]. On peut poursuivre le travail en observant que

${\displaystyle {\sqrt[{n}]{a^{m}}}=\left({\sqrt[{n}]{a}}\right)^{m}=\left(a^{m}\right)^{\frac {1}{n}}=\left(a^{\frac {1}{n}}\right)^{m}=a^{\frac {m}{n}}.}$

et vérifier que cette notation est compatible avec les propriétés déjà connues sur les exposants entiers.

C'est chez Newton que l'on voit apparaître pour la première fois un exposant fractionnaire. Mais Newton et Leibniz ne s'arrêteront pas là et se poseront même la question de travailler sur des exposants irrationnels sans être pour autant capables de leur donner un sens. Ce n'est qu'un siècle plus tard que ces notations prendront un sens précis avec la mise en place de la fonction exponentielle et la traduction :

${\displaystyle a^{\frac {1}{n}}=\exp \left({\frac {1}{n}}\ln a\right)}$ pour tout réel a strictement positif.

Fonction racine n-ième

Pour tout entier naturel non nul ${\displaystyle n}$, l'application ${\displaystyle x\mapsto x^{n}}$ est une bijection de ℝ₊ sur ℝ₊ dont l'application réciproque est la fonction racine n-ième. Il est donc loisible de construire sa représentation graphique, à l'aide de celle de la fonction puissance par symétrie d'axe la droite d'équation ${\displaystyle y=x}$.

On remarque que cette fonction est continue sur l'intervalle ${\displaystyle \left[0,+\infty \right[}$ et l'existence à l'origine d'une tangente confondue avec l'axe des y donc d'une non-dérivabilité en 0 ainsi qu'une branche parabolique d'axe (Ox).

Les formules sur la dérivée de la réciproque permettent d'établir que la fonction racine n-ième est dérivable sur l'intervalle ${\displaystyle \left]0,+\infty \right[}$ et que sa dérivée est ${\displaystyle x\mapsto {\frac {\sqrt[{n}]{x}}{nx}}}$, soit encore, avec l'exposant fractionnaire ${\displaystyle x\mapsto {\frac {1}{n}}x^{{\frac {1}{n}}-1}}$ montrant ainsi que la formule sur la dérivée d'une fonction puissance entière se généralise à celle d'une puissance inverse.

Développement en série entière

Le radical ou racine peut être représenté par la série de Taylor au point 1, qui s'obtient à partir de la formule du binôme généralisée : pour tout réel h tel que |h| ≤ 1,

${\displaystyle {\sqrt[{n}]{1-h}}=1-\sum _{k=1}^{\infty }a_{k}h^{k}{\text{ avec }}a_{k}={\frac {{\frac {1}{n}}\left(1-{\frac {1}{n}}\right)\left(2-{\frac {1}{n}}\right)\cdots \left(k-1-{\frac {1}{n}}\right)}{k!}}={\frac {\displaystyle \prod _{0<s<k}(sn-1)}{k!n^{k}}}\geq 0.}$

En effet, cette égalité, a priori seulement pour |h| < 1, assure en fait la convergence normale sur [–1, 1] puisque

${\displaystyle \sum _{k=1}^{\infty }a_{k}=\sup _{N\in \mathbb {N} ^{*}}\sum _{k=1}^{N}a_{k}=\sup _{N\in \mathbb {N} ^{*},h\in [0,1[}\sum _{k=1}^{N}a_{k}h^{k}=\sup _{h\in [0,1[}\sum _{k=1}^{\infty }a_{k}h^{k}=\sup _{h\in [0,1[}\left(1-{\sqrt[{n}]{1-h}}\right)=1<+\infty .}$

On peut remarquer (cf. « Théorème d'Eisenstein ») que tous les n^2k–1a_k sont entiers (dans le cas n = 2, ce sont les nombres de Catalan C_k–1).

Racines d'un complexe

Pour tout entier naturel non nul n, une racine n-ième d'un nombre complexe z est un nombre qui, élevé à la puissance donne z, c'est-à-dire une solution de l'équation

${\displaystyle x^{n}=z}$

d'inconnue x.

Lorsque z est différent de 0, il existe n racines n-ièmes distinctes de z. En effet, les racines n-ièmes d'un complexe z non nul sont aussi les racines du polynôme Xⁿ – z, qui admet bien n solutions dans l'ensemble des nombres complexes d'après le théorème de d'Alembert-Gauss.

Toutes les racines de n'importe quel nombre, réel ou complexe, peuvent être trouvées avec un simple algorithme. Le nombre doit d'abord être écrit sous la forme ${\displaystyle a{\rm {e}}^{{\rm {i}}\varphi }}$ (voir la formule d'Euler). Alors, toutes les racines n-ièmes sont données par :

${\displaystyle {\rm {e}}^{{\rm {i}}({\frac {\varphi +2k\pi }{n}})}\times {\sqrt[{n}]{a}}}$

pour ${\displaystyle k=0,1,2,\ldots ,n-1}$, où ${\displaystyle {\sqrt[{n}]{a}}}$ représente la racine n-ième principale de a.

Nombres réels positifs

Toutes les solutions complexes de ${\displaystyle x^{n}=a}$, autrement dit les racines n-ièmes de a, où a est un nombre réel positif, sont données par l'équation simplifiée :

${\displaystyle {\rm {e}}^{2\pi {\rm {i}}{\frac {k}{n}}}\times {\sqrt[{n}]{a}}}$

pour ${\displaystyle k=0,1,2,\ldots ,n-1}$, où ${\displaystyle {\sqrt[{n}]{a}}}$ représente la racine n-ième principale de a.

Racines de l'unité

Lorsque ${\displaystyle z=1}$, une telle racine s'appelle une racine n-ième de l'unité, et l'ensemble des racines n-ièmes de l'unité, noté ${\displaystyle {\mathcal {U}}_{n}}$, est formé des n racines du polynôme complexe

${\displaystyle X^{n}-1.}$

Il s'agit d'un sous-groupe cyclique du groupe multiplicatif des complexes de module 1. Il est formé des éléments ${\displaystyle \{1,{\rm {e}}^{{\rm {i}}{\frac {2\pi }{n}}},{\rm {e}}^{{\rm {i}}{\frac {4\pi }{n}}},\ldots ,{\rm {e}}^{{\rm {i}}{\frac {(2n-2)\pi }{n}}}\}}$

On appelle racine n-ième primitive de l'unité tout générateur du groupe cyclique ${\displaystyle {\mathcal {U}}_{n}}$. Ces racines primitives sont les éléments ${\displaystyle {\rm {e}}^{{\rm {i}}{\frac {2k\pi }{n}}}}$ où k est premier avec n. Leur nombre est égal à ${\displaystyle \varphi (n)}$ où ${\displaystyle \varphi }$ désigne l'indicatrice d'Euler.

Résolution par radicaux

Ludovico Ferrari a démontré que les racines des polynômes du quatrième degré pouvaient, comme pour ceux du deuxième et troisième degré, être calculées par radicaux, c'est-à-dire par un nombre fini d'opérations élémentaires sur les coefficients du polynôme, comportant des calculs de racines n-ièmes. Ceci n'est plus vrai en général pour les équations quintiques ou d'un degré supérieur, comme l'énonce le théorème d'Abel-Ruffini. Par exemple, les solutions de l'équation ${\displaystyle \ x^{5}=x+1}$ ne peuvent pas être exprimées en termes de radicaux.

Pour résoudre « numériquement » n'importe quelle équation du n-ième degré, voir l'algorithme de recherche de racines.

Racine en typographie

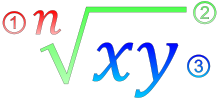
En typographie, une racine est composée de trois parties : le radical, l'indice et le radicande.

• Le radical est le symbole de la racine,
• l'indice est le degré de cette racine,
• enfin, le radicande est ce qu'il y a sous le radical.

Notes et références

Voir aussi

Articles connexes

• Algorithme de calcul de la racine n-ième
• Racines de fonctions polynomiales
• Algorithme de recherche d'un zéro d'une fonction
• Algorithme de la potence

Bibliographie

• (de) Ulrich Felgner, Mathematische Semesterberichte,vol. 52, n^o 1, 2005, Springer, p. 1-7, ISSN 0720-728X (Au sujet de l'origine du signe de racine)
• (de) Hans Kreul et Harald Ziebarth, Mathematik leicht gemacht, 6^e édition, 2006 Verlag Harri Deutsch. Le chapitre complet sur la racine avec des explications, des exemples et des exercices « disponible gratuitement en ligne »^{(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)} (ISBN 978-3-8171-1786-4)

• Portail des mathématiques