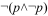Lambda-calcul simplement typé

Le lambda-calcul simplement typé est une variante du lambda-calcul qui se différencie de ce dernier par la présence de types. Il a été développé par Alonzo Church pour pallier l'incohérence du lambda-calcul non typé, due au paradoxe de Curry, et servir de fondements aux mathématiques.

Le lambda-calcul simplement typé partage un lien fort avec la logique propositionnelle minimale au travers de l'isomorphisme de Curry-Howard. Il peut également être vu comme une version simplifiée d'un langage de programmation fonctionnelle. De plus, toutes les fonctions définissables dans le lambda-calcul simplement typé terminent : le lambda-calcul est fortement normalisant.

Introduction

Le lambda-calcul pose comme primitive la notion de fonction. Si ${\displaystyle M}$ est une expression, ${\displaystyle \lambda x.M}$ représente la fonction ${\displaystyle f}$ définie par l'équation ${\displaystyle f(x)=M}$, et si ${\displaystyle M}$ et ${\displaystyle N}$ sont deux expressions, ${\displaystyle MN}$ désigne l'application de ${\displaystyle M}$ à ${\displaystyle N}$. Enfin, le lambda-calcul possède une notion dite de réduction qui correspond à effectuer une étape de calcul.

Par analogie, ${\displaystyle \lambda x.2x}$ pourrait désigner la fonction qui renvoie le double de son argument, et ${\displaystyle (\lambda x.2x)3\to 2\cdot 3\to 6}$ est la suite des étapes de calcul pour calculer cette fonction en ${\displaystyle 3}$. On peut définir et utiliser des types de données dans le lambda-calcul, notamment les entier naturels, les paires ou les listes. Néanmoins, tous les calculs ne terminent pas : ${\displaystyle \Omega =(\lambda x.xx)(\lambda x.xx)}$ présente la propriété que ${\displaystyle \Omega \to \Omega }$, et de plus, si ${\displaystyle F}$ est un terme, il existe un terme ${\displaystyle M}$ tel que ${\displaystyle FM\to ^{*}M}$. Pour reprendre l'analogie précédente, pour ${\displaystyle F=\lambda x.x+1}$, un tel ${\displaystyle M}$ vérifierait ${\displaystyle M=M+1}$, ce qui est impossible pour un entier naturel. L'introduction d'une discipline de types permet de résoudre ces deux problèmes, au prix d'une expressivité moindre.

Syntaxe

Il y a deux objets principaux dans le lambda-calcul simplement typé : les types, qui correspondent à des types de donnée en informatique et à des propositions en logique, et les termes qui correspondent à des programmes ou à des démonstrations.

Types

On suppose donné un ensemble de variables de types, qu'on note par des lettres grecques ${\displaystyle \alpha ,\beta ,\dots }$ Les types du lambda-calcul simplement typé sont désignés par les lettres ${\displaystyle T,U,\dots }$ et sont formés par^[1],[2] :

• Les variables de types ${\displaystyle \alpha ,\beta ,\ldots }$ ;
• Le type unité ${\displaystyle 1}$, qui possède un unique élément ;
• Si ${\displaystyle T}$ et ${\displaystyle U}$ sont des types, ${\displaystyle T\to U}$ est le type des fonctions de ${\displaystyle T}$ vers ${\displaystyle U}$ ;
• Si ${\displaystyle T}$ et ${\displaystyle U}$ sont des types, ${\displaystyle T\times U}$ est le produit des types ${\displaystyle T}$ et ${\displaystyle U}$, dont les éléments sont des paires composées d'un élément de ${\displaystyle T}$ et d'un de ${\displaystyle U}$.

Plus simplement,

${\displaystyle T,U,\ldots ::=\alpha ,\beta ,\ldots \;|\;1\;|\;T\to U\;|\;T\times U}$^{[note 1],[note 2]}

Termes

Les variables seront notées par des lettres minuscules ${\displaystyle x,y,\dots }$ tandis que les termes seront notés ${\displaystyle M,N,\dots }$ Les termes sont formés ainsi^[1],[2] :

• Les variables ${\displaystyle x,y,\ldots }$ sont des termes.
• L'unique terme du type unité est ${\displaystyle *}$.
• Si ${\displaystyle A}$ est un type et ${\displaystyle M}$ un terme, ${\displaystyle \lambda x^{A}.M}$ est un terme qui représente la fonction qui à ${\displaystyle x}$ de type ${\displaystyle A}$ associe l'expression ${\displaystyle M}$. On peut voir ça comme l'abstraction de ${\displaystyle x}$ dans l'expression ${\displaystyle M}$.
• Si ${\displaystyle M}$ et ${\displaystyle N}$ sont des termes, ${\displaystyle MN}$ est un terme qui correspond à l'application de la fonction ${\displaystyle M}$ à l'expression ${\displaystyle N}$.
• Si ${\displaystyle M}$ et ${\displaystyle N}$ sont des termes, ${\displaystyle \langle M,N\rangle }$ est un terme représentant la paire dont la première composante est ${\displaystyle M}$ et la deuxième ${\displaystyle N}$.
• Si ${\displaystyle M}$ est un terme et ${\displaystyle i=1~{\textrm {ou}}~2}$, ${\displaystyle \pi _{i}(M)}$ est un terme qui désigne la ${\displaystyle i}$-ème projection de la paire ${\displaystyle M}$.

Plus simplement,

${\displaystyle M,N,\ldots ::=x,y,\ldots \;|\;*\;|\;\lambda x^{A}.M\;|\;MN\;|\;\langle M,N\rangle \;|\;\pi _{1}(M)\;|\;\pi _{2}(M)}$

De plus, on considèrera que l'application est associative à gauche, c'est-à-dire qu'on notera ${\displaystyle MNO}$ pour ${\displaystyle (MN)O}$.

Règles de typage

On introduit la notation ${\displaystyle \Gamma \vdash M:A}$^[1], où ${\displaystyle \Gamma }$ est une liste de paires de la forme ${\displaystyle x:B}$ où ${\displaystyle x}$ est une variable et ${\displaystyle B}$ un type, ${\displaystyle M}$ est un terme et ${\displaystyle A}$ un type. Elle se lit « dans le contexte ${\displaystyle \Gamma }$, le terme ${\displaystyle M}$ a pour type ${\displaystyle A}$ ». Par exemple, ${\displaystyle x:A\vdash \lambda y:B.\langle x,y\rangle :B\to A\times B}$ se lit « si ${\displaystyle x}$ est une variable de type ${\displaystyle A}$, la fonction qui à ${\displaystyle y}$ de type ${\displaystyle B}$ associe la paire ${\displaystyle \langle x,y\rangle }$ est une fonction qui envoie les éléments de ${\displaystyle B}$ sur les paires de ${\displaystyle A}$ et de ${\displaystyle B}$ ».

Une règle de la forme ${\displaystyle {\frac {\Gamma _{1}\vdash M_{1}:A_{1}\dots \Gamma _{n}\vdash M_{n}:A_{n}}{\Gamma \vdash M:A}}}$ doit se comprendre comme « si ${\displaystyle \Gamma _{1}\vdash M_{1}:A_{1}}$, ..., ${\displaystyle \Gamma _{n}\vdash M_{n}:A_{n}}$alors ${\displaystyle \Gamma \vdash M:A}$ ». En particulier, ${\displaystyle {\frac {}{\Gamma \vdash M:A}}}$ signifie que ${\displaystyle \Gamma \vdash M:A}$ est toujours vrai.

${\displaystyle (var)\;{\frac {}{\Gamma ,x:A,\Gamma '\vdash x:A}}}$
${\displaystyle (abs)\;{\frac {\Gamma ,x:A\vdash M:B}{\Gamma \vdash \lambda x^{A}.M:A\to B}}}$			${\displaystyle (app)\;{\frac {\Gamma \vdash M:A\to B\quad \Gamma \vdash N:A}{\Gamma \vdash MN:B}}}$
${\displaystyle (pair)\;{\frac {\Gamma \vdash M:A\quad \Gamma \vdash N:B}{\Gamma \vdash \langle M,N\rangle :A\times B}}}$		${\displaystyle (\pi _{1})\;{\frac {\Gamma \vdash M:A\times B}{\Gamma \vdash \pi _{1}(M):A}}}$		${\displaystyle (\pi _{2})\;{\frac {\Gamma \vdash M:A\times B}{\Gamma \vdash \pi _{2}(M):B}}}$
${\displaystyle (*)\;{\frac {}{\Gamma \vdash *:1}}}$

Réduction

Tout comme le lambda-calcul non typé, le lambda-calcul simplement typé identifie les termes ${\displaystyle \alpha }$-équivalents et définit la substitution de façon similaire. De même, on peut définir pour le lambda-calcul simplement typé une notion de réduction^[3], qui représente une étape de calcul :

• ${\displaystyle (\lambda x.M)N\to _{\beta }M[x:=N]}$ ;
• ${\displaystyle \pi _{1}(\langle M,N\rangle )\to _{\beta }M}$ ;
• ${\displaystyle \pi _{2}(\langle M,N\rangle )\to _{\beta }N}$ ;
• ${\displaystyle \lambda x.Mx\to _{\eta }M}$ si ${\displaystyle x}$ n'est pas libre dans ${\displaystyle M}$ ;
• ${\displaystyle \langle \pi _{1}x,\pi _{2}x\rangle \to _{\eta }x}$ ;
• ${\displaystyle M\to _{\eta }*}$ si ${\displaystyle M}$ est de type ${\displaystyle 1}$.

Certaines règles sont étiquetées ${\displaystyle \beta }$, elles correspondent à des règles de calcul. La réduction associée est nommée ${\displaystyle \beta }$-réduction. D'autres sont étiquetées ${\displaystyle \eta }$, elles correspondent à des simplifications : si ${\displaystyle M\to _{\eta }N}$, ${\displaystyle M}$ et ${\displaystyle N}$ se « comportent » pareil. On nomme cette réduction ${\displaystyle \eta }$-réduction. On note ${\displaystyle M\to _{\beta \eta }N}$ si ${\displaystyle M\to _{\beta }N}$ ou ${\displaystyle M\to _{\eta }N}$ : c'est la ${\displaystyle \beta \eta }$-réduction.

Enfin, si ${\displaystyle \to _{R}}$ est une réduction, ${\displaystyle \to _{R}^{*}}$ est sa clôture réflexive et transitive et ${\displaystyle =_{R}}$ sa clôture réflexive, symétrique et transitive, c'est-à-dire que ${\displaystyle M\to _{R}^{*}N}$ s'il existe ${\displaystyle M_{1},\ldots ,M_{n}}$ tels que ${\displaystyle M=M_{1}\to _{R}\ldots \to _{R}M_{n}=N}$ et ${\displaystyle M=_{R}N}$ s'il existe ${\displaystyle M_{1},\ldots ,M_{n}}$ tels que ${\displaystyle M=M_{1}}$, ${\displaystyle M_{n}=N}$ et pour tout ${\displaystyle i}$ entre ${\displaystyle 1}$ et ${\displaystyle n-1}$, ${\displaystyle M_{i}\to _{R}M_{i+1}}$ ou ${\displaystyle M_{i}\leftarrow _{R}M_{i+1}}$.

Autoréduction

La ${\displaystyle \beta \eta }$-réduction possède la propriété d'autoréduction^[3] (ou subject reduction) : si ${\displaystyle \Gamma \vdash M:T}$ et ${\displaystyle M\to _{\beta \eta }N}$ alors ${\displaystyle \Gamma \vdash N:T}$. On peut voir cela comme une propriété de préservation du typage par la réduction.

Normalisation forte

Un terme est dit en forme normale s'il ne peut pas se réduire d'avantage^[4]. La ${\displaystyle \beta \eta }$-réduction possède la propriété de normalisation forte : tout terme peut se réduire, en un nombre fini d'étapes (potentiellement nul), en un terme en forme normale. On dit aussi qu'il est fortement normalisant. Si ${\displaystyle M\to _{R}^{*}N}$ et que ${\displaystyle N}$ est en forme normale pour ${\displaystyle \to _{R}}$, on dit que ${\displaystyle N}$ est une forme normale de ${\displaystyle M}$. Comme l’énonce le paragraphe suivant, cette forme est unique pour la ${\displaystyle \beta }$-réduction.

Confluence

Une réduction est dite confluente si pour tout termes ${\displaystyle M}$, ${\displaystyle N_{1}}$ et ${\displaystyle N_{2}}$ tels que ${\displaystyle M\to ^{*}N_{1}}$ et ${\displaystyle M\to ^{*}N_{2}}$, il existe un terme ${\displaystyle O}$ tel que ${\displaystyle N_{1}\to ^{*}O}$ et ${\displaystyle N_{2}\to ^{*}O}$. La ${\displaystyle \beta }$-réduction est confluente^[5], mais la ${\displaystyle \beta \eta }$-réduction ne l'est pas, comme le montre l'exemple suivant^[5], où ${\displaystyle x:A\times 1}$ :

• ${\displaystyle \langle \pi _{1}x,\pi _{2}x\rangle \to _{\eta }\langle \pi _{1}x,*\rangle }$ ;
• ${\displaystyle \langle \pi _{1}x,\pi _{2}x\rangle \to _{\eta }x}$ ;
• mais ${\displaystyle \langle \pi _{1}x,*\rangle }$ et ${\displaystyle x}$ sont tous deux en forme normale, donc ils ne peuvent pas se réduire vers un terme commun.

Si on considère le lambda-calcul simplement typé sans le type unité, la ${\displaystyle \beta \eta }$-réduction est confluente^[5].

La confluence assure l'unicité de la forme normale pour la ${\displaystyle \beta }$-réduction : en effet, supposons ${\displaystyle M\to _{\beta }^{*}N_{1}}$ et ${\displaystyle M\to _{\beta }^{*}N_{2}}$ avec ${\displaystyle N_{1}}$ et ${\displaystyle N_{2}}$ en forme normale. Si ${\displaystyle N_{1}\to _{\beta }^{*}O}$ alors ${\displaystyle N_{1}=O}$ puisque ${\displaystyle N_{1}}$ ne peut pas se réduire. De même, si ${\displaystyle N_{2}\to _{\beta }^{*}O}$ alors ${\displaystyle N_{2}=O}$. Donc ${\displaystyle N_{1}=N_{2}}$.

Cela signifie qu'en partant d'un terme donné, l'ordre des ${\displaystyle \beta }$-réductions n'importe pas : quel que soit l'ordre de réduction choisi, en un nombre fini d'étapes, on atteindra une forme normale qui ne dépend pas de l'ordre des réductions. En revanche, l'ordre de réduction peut avoir une influence sur le nombre de réductions. Par exemple, si ${\displaystyle y:A,t:B\vdash (\lambda x^{B}.y)((\lambda z^{B}.z)t)}$, alors ${\displaystyle (\lambda x^{B}.y)((\lambda z^{B}.z)t)\to y}$ atteint une forme normale en une étape en réduisant d'abord le premier rédex, tandis que ${\displaystyle (\lambda x^{B}.y)((\lambda z^{B}.z)t)\to (\lambda x^{B}.y)t\to y}$ atteint la même forme normale en deux étapes, en réduisant d'abord le deuxième rédex.

De plus, on peut choisir de faire les ${\displaystyle \eta }$-réductions après les ${\displaystyle \beta }$-réductions ou bien faire les ${\displaystyle \beta }$-réductions après les ${\displaystyle \eta }$-réductions : si ${\displaystyle M\to _{\eta }N\to _{\beta }O}$, alors le ${\displaystyle \beta }$-rédex réduit dans la deuxième réduction était déjà présent dans ${\displaystyle M}$, et si ${\displaystyle M}$ est en ${\displaystyle \beta }$-forme normale, il existe un terme ${\displaystyle N}$ (non nécessairement unique) en ${\displaystyle \beta \eta }$-forme normale tel que ${\displaystyle M\to _{\eta }^{*}N}$^[5].

Notes

Références

Bibliographie

• (en) Henk Barendregt, The Lambda Calculus : Its Syntax and Semantics, Amsterdam, North-Holland, coll. « Studies in Logic and the Foundations of Mathematics » (n^o 103), 1984, 621 p. (ISBN 978-0-444-87508-2, lire en ligne), Appendice A.
• Jean-Louis Krivine, Lambda-calcul : types et modèles, Masson, 1990, 206 p. (ISBN 978-2-225-82091-5, lire en ligne), chapitre 3, section 2.
• (en) Rob Nederpelt et Herman Geuvers, Type Theory and Formal Proof : An Introduction, Cambridge University Press, 2014 (ISBN 978-1-107-03650-5, DOI 10.1017/CBO9781139567725, lire en ligne). 
• (en) Peter Selinger, Lecture Notes on the Lambda Calculus, 2013, 2^e éd. (1^re éd. 2008), 120 p. (arXiv abs/0804.3434, lire en ligne). 

Articles connexes

• Système F

• Portail de l'informatique théorique
• Portail de la logique