Catalan's triangle

In combinatorial mathematics, Catalan's triangle is a number triangle whose entries ${\displaystyle C(n,k)}$ give the number of strings consisting of n X's and k Y's such that no initial segment of the string has more Y's than X's. It is a generalization of the Catalan numbers, and is named after Eugène Charles Catalan. Bailey^[1] shows that ${\displaystyle C(n,k)}$ satisfy the following properties:

1. ${\displaystyle C(n,0)=1{\text{ for }}n\geq 0}$.
2. ${\displaystyle C(n,1)=n{\text{ for }}n\geq 1}$.
3. ${\displaystyle C(n+1,k)=C(n+1,k-1)+C(n,k){\text{ for }}1<k<n+1}$
4. ${\displaystyle C(n+1,n+1)=C(n+1,n){\text{ for }}n\geq 1}$.

Formula 3 shows that the entry in the triangle is obtained recursively by adding numbers to the left and above in the triangle. The earliest appearance of the Catalan triangle along with the recursion formula is in page 214 of the treatise on Calculus published in 1800^[2] by Louis François Antoine Arbogast.

Shapiro^[3] introduces another triangle which he calls the Catalan triangle that is distinct from the triangle being discussed here.

General formula

The general formula for ${\displaystyle C(n,k)}$ is given by^[1][4]

${\displaystyle C(n,k)={\binom {n+k}{k}}-{\binom {n+k}{k-1}}}$

So

${\displaystyle C(n,k)={\frac {n-k+1}{n+1}}{\binom {n+k}{k}}}$

When ${\displaystyle k=n}$, the diagonal C(n, n) is the n-th Catalan number.

The row sum of the n-th row is the (n + 1)-th Catalan number, using the hockey-stick identity and an alternative expression for Catalan numbers.

Table of values

Some values are given by^[5]

k n	0	1	2	3	4	5	6	7	8
0	1
1	1	1
2	1	2	2
3	1	3	5	5
4	1	4	9	14	14
5	1	5	14	28	42	42
6	1	6	20	48	90	132	132
7	1	7	27	75	165	297	429	429
8	1	8	35	110	275	572	1001	1430	1430

Properties

• Formula 3 from the first section can be used to prove both

${\displaystyle C(n,k)=\sum _{i=0}^{k}C(n-1,i)=\sum _{i=k}^{n}C(i,k-1)}$

That is, an entry is the partial sum of the above row and also the partial sum of the column to the left (except for the entry on the diagonal).

• If ${\displaystyle k>n}$, then at some stage there must be more Y's than X's, so ${\displaystyle C(n,k)=0}$.

• A combinatorial interpretation of the ${\displaystyle (n,k-1)}$-th value is the number of non-decreasing partitions with exactly n parts with maximum part k such that each part is less than or equal to its index. So, for example, ${\displaystyle (4,2)=9}$ counts

${\displaystyle 1111,1112,1113,1122,1123,1133,1222,1223,1233}$

Generalization

Catalan's trapezoids are a countable set of number trapezoids which generalize Catalan’s triangle. Catalan's trapezoid of order m = 1, 2, 3, ... is a number trapezoid whose entries ${\displaystyle C_{m}(n,k)}$ give the number of strings consisting of n X-s and k Y-s such that in every initial segment of the string the number of Y-s does not exceed the number of X-s by m or more.^[6] By definition, Catalan's trapezoid of order m = 1 is Catalan's triangle, i.e., ${\displaystyle C_{1}(n,k)=C(n,k)}$.

Some values of Catalan's trapezoid of order m = 2 are given by

k n	0	1	2	3	4	5	6	7	8
0	1	1
1	1	2	2
2	1	3	5	5
3	1	4	9	14	14
4	1	5	14	28	42	42
5	1	6	20	48	90	132	132
6	1	7	27	75	165	297	429	429
7	1	8	35	110	275	572	1001	1430	1430

Some values of Catalan's trapezoid of order m = 3 are given by

k n	0	1	2	3	4	5	6	7	8	9
0	1	1	1
1	1	2	3	3
2	1	3	6	9	9
3	1	4	10	19	28	28
4	1	5	15	34	62	90	90
5	1	6	21	55	117	207	297	297
6	1	7	28	83	200	407	704	1001	1001
7	1	8	36	119	319	726	1430	2431	3432	3432

Again, each element is the sum of the one above and the one to the left.

A general formula for ${\displaystyle C_{m}(n,k)}$ is given by

${\displaystyle C_{m}(n,k)={\begin{cases}\left({\begin{array}{c}n+k\\k\end{array}}\right)&\,\,\,0\leq k<m\\\\\left({\begin{array}{c}n+k\\k\end{array}}\right)-\left({\begin{array}{c}n+k\\k-m\end{array}}\right)&\,\,\,m\leq k\leq n+m-1\\\\0&\,\,\,k>n+m-1\end{cases}}}$

( n = 0, 1, 2, ..., k = 0, 1, 2, ..., m = 1, 2, 3, ...).

Proofs of the general formula

Proof 1

This proof involves an extension of Andre's reflection method as used in the second proof for the Catalan number to different diagonals. The following shows how every path from the bottom left ${\displaystyle (0,0)}$ to the top right ${\displaystyle (k,n)}$ of the diagram that crosses the constraint ${\displaystyle n-k+m-1=0}$ can also be reflected to the end point ${\displaystyle (n+m,k-m)}$.

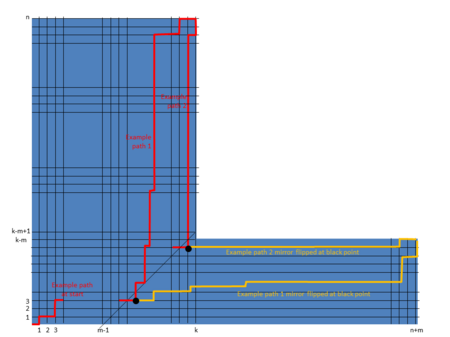
We consider three cases to determine the number of paths from ${\displaystyle (0,0)}$ to ${\displaystyle (k,n)}$ that do not cross the constraint:

(1) when ${\displaystyle m>k}$ the constraint cannot be crossed, so all paths from ${\displaystyle (0,0)}$ to ${\displaystyle (k,n)}$ are valid, i.e. ${\displaystyle C_{m}(n,k)=\left({\begin{array}{c}n+k\\k\end{array}}\right)}$.

(2) when ${\displaystyle k-m+1>n}$ it is impossible to form a path that does not cross the constraint, i.e. ${\displaystyle C_{m}(n,k)=0}$.

(3) when ${\displaystyle m\leq k\leq n+m-1}$, then ${\displaystyle C_{m}(n,k)}$ is the number of 'red' paths ${\displaystyle \left({\begin{array}{c}n+k\\k\end{array}}\right)}$ minus the number of 'yellow' paths that cross the constraint, i.e. ${\displaystyle \left({\begin{array}{c}(n+m)+(k-m)\\k-m\end{array}}\right)=\left({\begin{array}{c}n+k\\k-m\end{array}}\right)}$.

Therefore the number of paths from ${\displaystyle (0,0)}$ to ${\displaystyle (k,n)}$ that do not cross the constraint ${\displaystyle n-k+m-1=0}$ is as indicated in the formula in the previous section "Generalization".

Proof 2

Firstly, we confirm the validity of the recurrence relation ${\displaystyle C_{m}(n,k)=C_{m}(n-1,k)+C_{m}(n,k-1)}$ by breaking down ${\displaystyle C_{m}(n,k)}$ into two parts, the first for XY combinations ending in X and the second for those ending in Y. The first group therefore has ${\displaystyle C_{m}(n-1,k)}$ valid combinations and the second has ${\displaystyle C_{m}(n,k-1)}$. Proof 2 is completed by verifying the solution satisfies the recurrence relation and obeys initial conditions for ${\displaystyle C_{m}(n,0)}$ and ${\displaystyle C_{m}(0,k)}$.

References