Kreisverstärkung

Unter der Kreisverstärkung eines Regelkreises wird die statische Verstärkung des Reglers ${\displaystyle K_{R}}$ und der Regelstrecke ${\displaystyle K_{S}}$ für den „geschlossenen“ oder den „geöffneten“ Regelkreis als unterschiedliche Anwendungen verstanden.

In der Regelungstechnik wird häufig für die Beschreibung dynamischer Systeme sowie deren Komponenten das Verfahren der Übertragungsfunktion G(s) angewendet, welches sich auf Laplace-transformierte Differenzialgleichungen der Systeme beziehen.

Die Übertragungsfunktion (Bildbereich) wird algebraisch behandelt und kann auch in den Originalbereich zurück transformiert werden.^[1]

In erster Linie interessiert bei der Konzeption eines Regelkreises dessen Stabilität, zulässige Regelabweichung und das Einschwingverhalten der Regelgröße y(t) als Funktion der Führungsgröße w(t). Diese Größen sind von der statischen Kreisverstärkung, sowie von weiteren dynamischen Regelkreis-Elementen wie Integratoren ${\displaystyle I_{1}}$-Gliedern und ${\displaystyle PD_{1}}$-Gliedern abhängig.

Einfache grafische Verfahren der Stabilitätsbestimmung sind die Ortskurve des Frequenzgangs und das Bodediagramm.

Die numerische Berechnung der Regelkreisglieder mit Differenzengleichungen erlaubt die näherungsweise Darstellung des zeitlichen Verlaufs der Regelgröße Y(k) als Funktion der Eingangsgröße W(k) in Form von nummerierten Zahlenwerten ${\displaystyle k=[0,1,2,3,\dotsc ,k_{\text{max}}]}$ im Abstand ${\displaystyle \Delta t}$.

Übliche mathematische Verfahren der Berechnung eines Regelkreises

Das Blockschaltbild eines Regelkreises kann mit mathematischen Modellen:

• gewöhnlichen Differenzialgleichungen ${\displaystyle f(t)}$,
• mit der Übertragungsfunktionen ${\displaystyle G(s)}$ oder alternaiv mit dem Frequenzgang ${\displaystyle F(j\omega )}$,
• numerisch mit Differenzengleichungen (Differenzenverfahren) über Differenzenquotienten ${\displaystyle y'(t)={\frac {dy}{dt}}\approx {\frac {y_{k+1}-y_{k}}{\Delta t}}}$.

dargestellt und beschrieben werden.

Regelkreisverstärkung des aufgeschnittenen Regelkreises

Die Betrachtung des offenen Regelkreises als Reihenschaltung (Produktdarstellung) hat einige Vorteile für den Regelkreisentwurf:

• Die Rückführung der Ausgangsgröße, die Regelgröße ${\displaystyle y(t)}$, wird gedanklich oder in praxi vor der Regeldifferenz des Soll-Istwert-Vergleiches ${\displaystyle w(t)=e(t)-y(t)}$ unterbrochen. (Ohne Messglied in der Rückführung).
• Damit wird die Führungsgröße ${\displaystyle w(t)}$ die Eingangsgröße des aufgeschnittenen Regelkreises und die Ausgangsgröße ${\displaystyle y(t)}$ zu einer Steuerkette in Reihenschaltung.
• Die Übertragungsfunktion ${\displaystyle G_{0}(s)}$ eines Beispiels mit einem Regler und einer Regelstrecke lautet mit der Verstärkung des P-Reglers ${\displaystyle K_{R}}$ und der Verstärkung der Regelstrecke ${\displaystyle K_{S}}$ und 3 Verzögerungsgliedern 1. O. des offenen Regelkreises:

${\displaystyle G_{0}(s)=G_{R}(s)\cdot G_{S}(s)=K_{R}\cdot {\frac {K_{S}}{(T_{1}\cdot s+1)(T_{2}\cdot s+1)(T_{3}\cdot s+1)}}}$.

Aus dieser Gleichung ist die statische Kreisverstärkung ${\displaystyle K_{R}\cdot K_{S}}$ deutlich erkennbar. Übertragungsglieder in der Rückführung, sofern vorhanden, multiplizieren sich mit dem Regler und der Strecke.

Ein ${\displaystyle I_{1}}$-Glied ${\displaystyle {\frac {U}{E}}(s)={\frac {1}{T_{N}\cdot s}}={\frac {K_{I}}{s}}}$ als alleinstehendes Glied ${\displaystyle G_{I}(s)}$ darf nicht in der Signalkette enthalten sein, anderenfalls läuft die Ausgangsgröße ${\displaystyle Y(s)}$ bzw. ${\displaystyle (y(t))}$ in die Begrenzung.

• Bestimmung der Regler-Parameter

Aus der Übertragungsfunktion des offenen Regelkreises können unmittelbar weitere Regelparameter des Reglers für den geschlossenen Regelkreis ermittelt werden, indem durch Kompensation der Verzögerungsglieder ${\displaystyle PT1}$ der Regelstrecke mit einzufügenden ${\displaystyle PD1}$-Gliedern des Reglers bei gleichen Zeitkonstanten ${\displaystyle T=T_{v}}$ vorgenommen wird.

Für diesen Fall, dass nur noch ein PT1-Glied im geschlossenen Regelkreis noch wirksam ist, kann theoretisch eine unendlich hohe K-Verstärkung gewählt werden, ohne eine Schwingneigung der Regelgröße befürchten zu müssen.

Diese Beziehung gilt für das „ideale“ ${\displaystyle PD1}$-Glied, das technisch als Hardware nicht realisierbar ist. Es ist nicht möglich, z. B. für einen Eingangssprung ${\displaystyle e(t)}$, ein Ausgangssignal ${\displaystyle u(t)}$ mit unendlich großer Amplitude zu realisieren.

Reale ${\displaystyle PD1}$-Glieder enthalten zusätzlich eine kleine Verzögerung z. B. ${\displaystyle T_{p}<{\frac {T}{10}}}$.

${\displaystyle \to }$ Siehe Artikel Regler.

• Stabilitätsbedingung mit der Ortskurve des Frequenzgangs des offenen Regelkreises

Wird beim Durchlaufen der Ortskurve des offenen Regelkreises ${\displaystyle Fo(j\omega )}$ in Richtung steigender Werte von ${\displaystyle \omega }$ der kritische Punkt (−1; j0) auf der linken (negativen) Seite der Achse der Realteile nicht umschlungen bzw. berührt, ist der geschlossene Regelkreis stabil.

• Stabilitätsbedingung im Bode-Diagramm des offenen Regelkreises mit dem vereinfachten Stabilitätskriterium von Nyquist

Ein geschlossener Regelkreis ist stabil, wenn die nacheilende Phasenverschiebung ${\displaystyle \varphi }$ vom Ausgangs- zum Eingangssignal des offenen Regelkreises bei der Kreisverstärkung ${\displaystyle K=1}$ und ${\displaystyle \varphi >-180\ Grad}$ beträgt.

Kreisverstärkung des geschlossenen Regelkreises

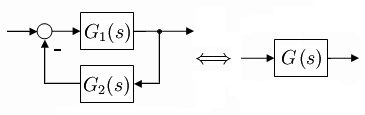
• Blockschaltbild der Gegenkopplung bzw. Rückkopplung von 2 Übertragungsfunktionen:

• Gleichung der Übertragungsfunktion ${\displaystyle G(s)}$ für ein Meßglied ${\displaystyle G_{2}(s)}$ in der Rückführung:^[2]

${\displaystyle G(s)={\frac {Y(s)}{W(s)}}={\frac {G_{1}(s)}{1+G_{1}(s)\cdot G_{2}(s)}}}$.

• Ist das Messglied ${\displaystyle G_{2}(s)}$ in der Rückführung nicht vorhanden, dann lautet die Übertragungsfunktion für G(s) des geschlossenen Kreises:

${\displaystyle G(s)={\frac {Y(s)}{W(s)}}={\frac {G_{1}(s)}{1+G_{1}(s)}}}$.

• Übertragungsfunktion eines Beispiels für einen Regelkreis mit ${\displaystyle G_{0}}$ gleich 2 Verzögerungsgliedern und Verstärkungsfaktoren (PT1-Gliedern, offener Regelkreis):

Das Störglied D(s) kann sich statisch oder dynamisch verhalten und wird hier nicht betrachtet.

${\displaystyle G_{0}(s)=G_{R}(s)\cdot G_{S}(s)=K_{R}\cdot {\frac {K_{S}}{(T1\cdot s+1)(T2\cdot s+1)}}}$.

Wird in den offenen Regelkreis G1(s) ein „ideales“ PD1-Glied:

${\displaystyle {\frac {U}{E}}{(s)}=K_{PD}+K_{PD}\cdot T_{V}\cdot s=(T_{V}\cdot s+1)\qquad \qquad K_{PD}=1}$

eingefügt mit gleicher Zeitkonstante ${\displaystyle T_{V}=T2}$, dann kompensieren sich das PT2-Glied mit dem PD1-Gied zu dem Faktor 1.

Die Übertragungsfunktion des offenen Kreises lautet dann mit dem PD1-Glied im Regler:

${\displaystyle G_{0}(s)=G_{R}(s)\cdot G_{S}(s)={\frac {K_{R}\cdot {K_{S}}\cdot (T_{V}\cdot s+1)}{(T_{1}\cdot s+1)\cdot (T_{2}\cdot s+1)}}={\frac {K_{R}\cdot {K_{S}}}{(T_{1}\cdot s+1)}}}$.

Die Übertragungsfunktion des geschlossenen Regelkreises lautet damit:

${\displaystyle G(s)={\frac {Y(s)}{W(s)}}={\frac {G_{1}(s)}{1+G_{1}(s)}}={\frac {\frac {K_{R}\cdot K_{S}}{T_{1}\cdot s+1}}{1+{\frac {K_{R}\cdot K_{S}}{T_{1}\cdot s+1}}}}={\frac {{K_{R}}\cdot {K_{S}}}{{(T_{1}\cdot s+1)}+K_{R}\cdot K_{s}}}}$.

• Darstellung der Führungs-Übertragungsfunktion für den geschlossenen verzögerungsfreien Regelkreis: Störgröße D = 0.

${\displaystyle K={\frac {y}{w}}={\frac {K_{R}\cdot K_{s}}{1+K_{R}\cdot K_{S}}}}$.

Aus dieser Darstellung wird das statische Verhalten der Ausgangsgröße y(t) eines Regelkreises mit einem P-Regler deutlich. Die Regelgröße y(t) erreicht je nach Größe der Kreisverstärkung ${\displaystyle K_{R}}$ und ${\displaystyle K_{S}}$ nicht den Wert der Führungsgröße ${\displaystyle w(t)}$, weil ${\displaystyle K<1}$. Bei großer ${\displaystyle K_{R}}$-Verstärkung wird ${\displaystyle K\approx 1}$.

Bei diesem Beispiel eines Regelkreises mit einem Verzögerungsglied kann ${\displaystyle K_{R}}$ beliebig hoch gewählt werden, denn es handelt sich hier mit dem Einsatz eines P-Reglers um einen schnellen, genauen, schwingfreien Regelkreis.

In der Hardware-Praxis wird man keine unbegrenzten P-Regler-Verstärkungen realisieren können, weil reale PD1-Glieder eine kleine Verzögerung aufweisen müssen.

• Numerische Berechnung der Regelgröße ${\displaystyle y_{k}}$

Sämtliche Übertragungsglieder des Reglers und der Strecke werden über Differenzengleichungen numerisch berechnet. Der zeitliche Verlauf der Regelgröße ${\displaystyle y_{k}}$ als Funktion der Eingangsgröße ${\displaystyle w_{k}}$ (Führungsgröße) ergibt sich für den geschlossenen Regelkreis mit der Schließbedingung ${\displaystyle e(k)=w(k)-y(k)}$.

Eine Differenzengleichung ist eine numerisch lösbare rekursive Berechnungsvorschrift für eine diskret definierte Wertefolge von nummerierten Folgeelementen bzw. Stützstellen ${\displaystyle y_{k}}$ im Abstand eines meist konstanten Intervalls ${\displaystyle \Delta t}$.^[3]

Je höher die Anzahl der Wertefolgen in einem Zeitbereich ${\displaystyle k_{max}\cdot \Delta t}$ gewählt wird, um so höher ist die Genauigkeit der Berechnung. Rundungsfehler bei nicht ausreichender Stellengenauigkeit addieren sich bei jedem Folgeglied.

${\displaystyle \to }$ Siehe Artikel Differenzengleichung (Differenzenverfahren)

Anwendungen

In der Regelungstechnik können über die Kreisfrequenz bestimmte Eigenschaften des Regelkreises optimiert werden. Die Elektrotechnik kennt den konzeptionell ähnlichen Begriff der Schleifenverstärkung, die das Verhalten rückgekoppelter elektronischer Schaltungen bestimmt. In der biomedizinischen Kybernetik wird das Konzept der Kreisfrequenz bei Haltereglern als Dispositionsindex bezeichnet. Mit Dispositionsmetriken wird z. B. die Güte der Insulin-Glukose-Homöostase beurteilt.

Einzelnachweise

1. ↑ Lutz, Wendt: Taschenbuch der Regelungstechnik. Mit MATLAB und Simulink. 11., ergänzte Auflage. Verlag Europa-Lehrmittel, Haan-Gruiten 2019, ISBN 978-3-8085-5869-0, Hauptkapitel: Mathematische Transformationen. Unterkapitel: Original- und Bildbereich.
2. ↑ Lutz, Wendt: Taschenbuch der Regelungstechnik. Mit MATLAB und Simulink. 11., ergänzte Auflage. Verlag Europa-Lehrmittel, Haan-Gruiten 2019, ISBN 978-3-8085-5869-0, Hauptkapitel: Berechnung von Regelkreisen mit Proportionalelementen.
3. ↑ Lutz, Wendt: Taschenbuch der Regelungstechnik. Mit MATLAB und Simulink. 11., ergänzte Auflage. Verlag Europa-Lehrmittel, Haan-Gruiten 2019, ISBN 978-3-8085-5869-0, Hauptkapitel: Mathematische Methoden zur Berechnung von digitalen Regelkreisen. Unterkapitel: Differenzengleichungen.

Weblinks

• Akademie Raddy: P-Regler ► Beispiel Heizung ► Kreisverstärkung berechnen mit Formel für Regeldifferenz. Video.

Literatur

• Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik. Mit MATLAB und Simulink. 12., ergänzte Auflage. Verlag Europa-Lehrmittel, Haan-Gruiten 2021, ISBN 978-3-8085-5870-6.
• Jan Lunze: Regelungstechnik. 2 Bände.
  • (Band) 1: Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen. 6. Auflage. Springer, Berlin u. a. 2007, ISBN 978-3-540-70790-5;
  • (Band) 2: Mehrgrößensysteme, Digitale Regelung. 4. Auflage. Springer, Berlin u. a. 2006, ISBN 3-540-32511-5.